Capítulo 6 Segmentação

A segmentação subdivide uma imagem para detecção de regiões ou objetos para uma determinada aplicação. Os principais métodos de segmentação utilizam a distribuição dos valores de intensidade, seja pelos padrões de similaridade, ou de descontinuidade [2, p. 454]. Nas técnicas de similaridade, as imagens são divididas em regiões semelhantes com base em um conjunto de características. Na segmentação por descontinuidade se consideram as mudanças abruptas de intensidades, caracterizadas por pontos isolados, linhas ou bordas na imagem.

6.1 Detecção por descontinuidade

Bordas podem ser descritas como o limite ou a fronteira entre duas regiões onde ocorre uma variação brusca de intensidade em uma determinada direção. Uma linha pode ser vista como um segmento de borda em que a intensidade do fundo de cada lado da linha ou é muito superior, ou muito inferior à intensidade dos pixels da linha. Linhas com o comprimento e largura iguais a um pixel são tratados como pontos isolados [2, p. 456]. Os métodos de detecção de bordas se baseiam no comportamento das derivadas, que podem detectar mudanças locais abruptas. Em uma função digital, as derivadas são aproximadas como termos de diferenças. Aproximações podem ser obtidas por meio de expansões em séries de Taylor, como demonstrado no livro “Processamento digital de imagens” [2, p. 457], em que os resultados para a primeira e a segunda ordem no ponto \(x\) pode ser obtido pelas Equações (6.1) e (6.2) respectivamente:

\[\frac{\delta f}{\delta x} = f'(x) = f(x+1) - f(x) \tag{6.1}\] \[\frac{\delta^2 f}{\delta x^2} = f''(x) = f(x+1) + f(x-1) - 2f(x) \tag{6.2}\]

Para avaliar o comportamento das derivadas na transição de intensidades apresentamos na Figura 6.1 um perfil de intensidade horizontal (linha de digitalização) de uma imagem, juntamente com os resultados das duas últimas equações, (6.1) e (6.2), para alguns pontos. A imagem contém vários objetos sólidos, uma linha e um ponto interno de ruído, e a linha de digitalização está próxima ao centro, incluindo o ponto isolado. A Figura 6.1(c) mostra uma simplificação do perfil e como as derivadas de primeira e segunda ordem se comportam quando encontram um ponto isolado, uma linha e as bordas dos objetos.

Com base nos resultados das Equações (6.1) e (6.2), na Figura 6.1, observa-se que atendem as propriedades das derivadas. No início e ao longo da rampa de intensidade, a derivada de primeira ordem é diferente de zero, enquanto a segunda derivada é diferente de zero apenas no início e no final da rampa. Estes comportamentos indicam que as derivadas de primeira ordem produzem bordas grossas, e as de segunda ordem produzem bordas mais finas [2, p. 458].

Figura 6.1: (a) Imagem. (b) Perfil de intensidade horizontal no centro da imagem. (c) Perfil simplificado e resultados das derivadas. [2, p. 457].

No ponto de ruído, a resposta para a derivada de segunda ordem é mais forte do que para a primeira derivada. Derivadas de segunda ordem acentuam as respostas em mudanças bruscas, podendo melhorar pequenos detalhes [2, p. 458]. Na linha com detalhes bem finos, a derivada de segunda ordem também tem maior magnitude. Nota-se nas bordas em rampa e nas bordas em degrau, que a segunda derivada tem sinais opostos (negativo para positivo ou vice-versa) conforme entra e sai da borda, o que caracteriza uma “borda dupla”. O sinal da segunda derivada também pode ser utilizado para determinar se uma transição em uma borda é de claro para escuro (segunda derivada negativa) ou de escuro para claro (segunda derivada positiva) [2, p. 458].

6.1.1 Detecção de pontos isolados

Considerando que as derivadas de segunda ordem têm uma resposta mais forte aos detalhes finos, o operador diferencial laplaciano (6.3)

\[\nabla^2f(x,y) = \frac{\partial^2f}{\partial x^2} + \frac{\partial^2f}{\partial y^2} \tag{6.3}\] é ideal para a detecção de pontos [2, p. 459]. As aproximações das derivadas de segunda ordem por termos de diferenças vistas podem ser estendidas para os dois termos do laplaciano (6.4) e (6.5)

\[\frac{\partial^2f}{\partial x^2} = f(x+1, y) + f(x-1, y) -2f(x,y) \tag{6.4}\] \[\frac{\partial^2f}{\partial y^2} = f(x, y+1) + f(x, y-1) -2f(x,y) \tag{6.5}\]

Ao se relacionar essas três últimas equações, (6.3), (6.4) e (6.5), obtém-se o laplaciano discreto (6.6): \[\nabla^2f(x,y) = f(x+1, y) + f(x-1, y) + f(x, y+1) + f(x, y-1) -4f(x,y) \tag{6.6}\]

Essa equação pode ser implementada utilizando a máscara de filtragem identificada na Figura 6.2(a). Para incluir as direções diagonais na definição do laplaciano digital, acrescenta-se mais dois termos a esta equação, (6.6), um para cada direção diagonal. A Figura 6.2(b) mostra a máscara de filtragem desta atualização que inclui as diagonais.

Figura 6.2: (a) Máscara referente a equação laplaciana discreta. (b) Máscara que inclui as diagonais. [2, p. 106]

A intensidade de um ponto isolado será muito diferente do seu entorno, portanto, ao aplicar a máscara, as únicas diferenças de intensidade relevantes serão as mais altas, maiores que um limite determinado (\(T\)) para serem consideradas pontos isolados [2, p. 459]. Para detectar o ponto se utiliza a seguinte expressão (6.7):

\[ g(x,y) = \begin{cases} 1,\ se\ R(x,y) \geq T \\0,\ caso\ contrário \end{cases} \tag{6.7} \] em que \(g\) é a imagem de saída, \(T\) é um limiar não negativo e \(R\) é o operador laplaciano. O ponto isolado será detectado no local \((x, y)\) em que a máscara está centrada se o módulo da resposta nesse ponto exceder o limiar estabelecido. Os pontos detectados são rotulados como 1 na imagem de saída, e os demais como 0, o que produz uma imagem binária.

6.1.2 Detecção de linhas

Semelhante à detecção de pontos isolados, as derivadas de segunda ordem geram respostas mais fortes na detecção de linhas, e produzem linhas mais finas do que as derivadas de primeira ordem [2, p. 460]. Ao utilizar a máscara laplaciana da Figura 6.2 sobre a imagem de um componente em um circuito eletrônico (parte de uma conexão wire-bond), representado na Figura 6.3(a), obtém-se como resultado a Figura 6.3(b). Na seção ampliada da Figura 6.3(b), as linhas mais claras identificam os pontos positivos, o cinza escuro são os valores negativos, e o cinza médio representa zero. O efeito de linha dupla é evidente na região ampliada ao se utilizar a segunda derivada.

Figura 6.3: (a) Imagem do circuito. (b) Resultado do filtro laplaciano. (c) Valor absoluto do filtro laplaciano. (d) Valores positivos do filtro laplaciano. [2, p. 460]

Para destacar as linhas após a aplicação do filtro e remover os valores negativos pode ser utilizado o módulo dos valores calculados ou utilizar apenas os valores positivos do laplaciano [2, p. 460], os resultados destas metodologias estão identificados na Figura 6.3(c) e (d), respectivamente. Nota-se que as linhas geradas pela abordagem do módulo são mais grossas, pois a espessura é o dobro se comparada com a outra metodologia. Nas duas situações, as linhas mais largas que o tamanho do filtro laplaciano são separadas por um “vale” de zeros. A detecção de linhas é ideal quando a espessura é menor que o detector, ao contrário se recomenda tratar o elemento como uma região e utilizar outros métodos [2, p. 460].

O filtro laplaciano, na Figura 6.2, é isotrópico, assim, a sua resposta independe da direção [2, p. 460]. No caso das linhas, pode ser interessante a detecção em apenas uma determinada direção, utilizando, por exemplo, uma das máscaras apresentadas na Figura 6.4. Para a primeira máscara da Figura 6.4, os sinais mais fortes ocorrem em linhas horizontais da imagem que passam pela linha do meio da máscara. O segundo filtro detecta melhor as linhas com \(45°\) de inclinação. O terceiro filtro para linhas verticais. O quarto filtro para linhas com \(-45º\) de inclinação. Vale destacar que estamos utilizando a convenção de que os eixos da imagem têm sua origem no canto superior esquerdo, com o eixo \(x\) positivo apontando para baixo e o eixo \(y\) positivo se estendendo à direita. Os ângulos das linhas são medidos em relação ao eixo \(x\) positivo.

Figura 6.4: Máscaras para detecção de linhas em uma determinada direção [2, p. 461].

Quando o objetivo é detectar todas as linhas da imagem em uma direção específica, aplica-se a máscara associada a essa direção e se define um limiar (\(T\)) para selecionar os sinais mais fortes. Para os quatro últimos filtros apresentados, as linhas de 1 pixel de espessura apresentam os maiores resultados [2, p. 462].

6.2 Detecção de Bordas

6.2.1 Modelos de Bordas

Na Figura 6.5, estão os principais modelos de borda, que são classificados de acordo com os perfis de intensidade. A primeira borda, borda em degrau, (a), apresenta uma transição entre dois níveis de intensidade e são consideradas ideais com uma distância de 1 pixel. Na prática, as bordas nas imagens digitais não apresentam uma transição tão bem definida, assim, modelos mais apropriados consideram um perfil de rampa como da Figura 6.5(b) [2, p. 462]. Quanto mais indefinida é a transição da borda, menor é a inclinação da rampa. Em vez de uma borda com 1 pixel de espessura, todos os pontos na rampa fazem parte da borda. Além disso, na Figura 6.5, mostra os modelos de bordas com seus respectivos perfis de intensidade.

Figura 6.5: (a) Borda degrau. (b) Borda rampa. (c) Borda telhado. [2, p. 462]

No terceiro modelo de borda, Figura 6.5(c), em forma de telhado ou roof edge, a base (largura) de uma borda é definida pela espessura e a nitidez da linha. Quando a base é igual 1 pixel de espessura, uma borda em forma de telhado é definida como uma linha [2, p. 462].

As imagens da Figura 6.6 não apresentam ruídos, entretanto os modelos de detecção devem considerar que as bordas estejam desfocadas e com ruídos. Na primeira coluna da Figura 6.5 estão quatro bordas de perfil rampa com diferentes níveis de ruídos, e abaixo de cada imagem, está o perfil horizontal de intensidade que passa pelo centro da imagem. A primeira imagem no canto esquerdo não apresenta ruído, e as outras três imagens da primeira coluna foram alteradas com ruído gaussiano aditivo com média zero e desvio padrão de \(0.1\), \(1.0\) e \(10.0\) níveis de intensidade, respectivamente.

Figura 6.6: Primeira coluna: imagens e perfis de intensidade de uma borda em declive corrompida pelo ruído gaussiano aleatório de desvio padrão \(0.0\), \(0.1\), \(1.0\) e \(10.0\) níveis de intensidade, respectivamente. Segunda coluna: imagens da primeira derivada. Terceira coluna: imagens da segunda derivada. [2, p. 465]

Na segunda e terceira coluna estão identificados, respectivamente, a primeira e a segunda derivada dos perfis de intensidade da primeira coluna. A primeira derivada é utilizada para detectar bordas, pois identifica pontos de transição abrupta de intensidade na imagem. Para o resultado da primeira derivada na primeira linha, os valores na rampa são positivos e, nas regiões de intensidade constante é igual a zero. As duas faixas pretas na imagem da parte superior da coluna central são os resultados iguais a zero da primeira derivada, e os valores constantes estão identificados como cinza claro.

Como as bordas são uma transição de uma região escura para uma região branca, a segunda derivada na terceira coluna é positiva no início da rampa e negativa no final. A linha que passa por estes dois resultados da derivada se intercepta com o eixo de intensidade zero, gerando o ponto de cruzamento por zero que é utilizado para localizar o centro de bordas espessas [2, p. 464]. Nas regiões de intensidade constante, as derivadas de segunda ordem também são zero, e se apresentam na cor cinza claro nas imagens da terceira coluna. As linhas finas verticais brancas e pretas são os resultados positivos e negativos da segunda derivada.

Mesmo não sendo perceptível os ruídos nas imagens da segunda e terceira linha, eles apresentaram um impacto significativo nas derivadas, principalmente na derivada de segunda ordem que é mais sensível a eles. Quanto maior o ruído, mais difícil de se associar com os perfis das derivadas, dificultando a detecção de bordas. Este comportamento pode ser tratado com a suavização da imagem em uma etapa anterior a segmentação [2, p. 464].

6.2.2 Método do gradiente (Roberts, Prewitt, Sobel)

Na detecção de bordas, as derivadas de primeira ordem são calculadas utilizando a magnitude do gradiente, que é um vetor cuja a direção indica os pontos de maior variação de intensidade [3, p. 155]. A Figura 6.7 indica que a direção do gradiente sempre será perpendicular à direção tangente da borda. Para uma função \(f(x, y)\), o gradiente de \(f\) nas coordenadas \((x, y)\) na forma matricial é expresso como a Equação (6.8)

\[\nabla f = \begin{bmatrix} G_x \\ G_y \end{bmatrix} = \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix} \tag{6.8}\]

Figura 6.7: Vetor gradiente \(\nabla f\) em uma borda. [3, p. 155]

O módulo ou magnitude (tamanho) do vetor \(\nabla f\) é dado como \(M(x,y)\), Equação (6.9). \[M(x,y) = \sqrt{G^2_x + G^2_y} \tag{6.9}\]

O módulo do gradiente é a maior taxa de variação de \(f(x,y)\) na direção do vetor gradiente. Devido ao custo computacional, a magnitude do gradiente é aproximada pelo uso dos valores absolutos, Equação (6.10) [3, p. 155]. \[M(x,y) \simeq |G_x| + |G_y| \tag{6.10}\]

A direção do vetor gradiente é dada pela Equação (6.11), que retorna um ângulo \[ \alpha(x,y) = tg^{-1} \begin{bmatrix} \frac{G_y}{G_x} \end{bmatrix} \tag{6.11}\]

medido em relação ao eixo \(x\). Da mesma forma que a magnitude \(M(x, y)\), ou imagem gradiente, o ângulo \(\alpha(x, y)\) também é uma imagem do mesmo tamanho que a original formado pela divisão da imagem \(G_y\) por \(G_x\) [2, p. 466].

Para calcular as derivadas parciais \(\partial f/ \partial x\) e \(\partial f/ \partial y\) no caso de quantidades digitais, é necessário utilizar aproximações discretas e, em seguida, determinar as máscaras de filtragem correspondentes. Uma forma de aproximação é considerar a diferença entre os elementos da vizinhança para calcular a magnitude do gradiente [3, p. 157]. Ao se utilizar as diferenças cruzadas, como na seguinte Equação (6.12)

\[M(x,y) \simeq |f(x,y) - f(x+1, y+1)| + |f(x,y+1) - f(x+1, y)| \tag{6.12}\] é o mesmo que aplicar os filtros de tamanho 2x2 da Figura 6.8 e somar os resultados absolutos.

Figura 6.8: Operador de Roberts [3, p. 157].

Estes operadores, conhecidos como operadores de Roberts, foram uma das primeiras tentativas de usar máscaras 2-D, entretanto não são tão úteis quanto as máscaras simétricas ao redor do ponto central, em que as menores são de tamanho 3×3 [2, p. 467]. As aproximações mais simples para as derivadas parciais usando máscaras de tamanho 3×3 são dadas pela Equação (6.13)

\[ \begin{split} M(x,y) &\simeq |[f(x+1,y-1) + f(x+1,y) + f(x+1,y+1)]-\\ &\ \ \ \ \ [f(x-1,y-1) + f(x-1,y) + f(x-1,y+1)]+\\ &\ \ \ \ \ [f(x-1,y+1) + f(x,y+1) + f(x+1,y+1)]-\\ &\ \ \ \ \ [f(x-1,y-1) + f(x,y-1) + f(x+1,y-1)]| \end{split} \tag{6.13}\]

Figura 6.9: Operador de Prewitt [3, p. 158].

A Equação anterior, (6.8), pode ser implementada aplicando as máscaras da Figura 6.9, que recebem o nome de operadores de Prewitt. Uma variação deste último método utiliza o valor \(2\) como peso no centro do coeficiente [3, p. 158]

\[ \begin{split} M(x,y) &\simeq |[f(x+1,y-1) + 2f(x+1,y) + 2f(x+1,y+1)]-\\ &\ \ \ \ \ [f(x-1,y-1) + 2f(x-1,y) + f(x-1,y+1)]+\\ &\ \ \ \ \ [f(x-1,y+1) + 2f(x,y+1) + f(x+1,y+1)]-\\ &\ \ \ \ \ [f(x-1,y-1) + 2f(x,y-1) + f(x+1,y-1)]| \end{split} \tag{6.14}\]

Figura 6.10: Operador de Sobel [3, p. 158].

O resultado das equação pode ser obtido com a soma dos valores absolutos dos resultados das máscaras na Figura 6.10, chamadas de operadores de Sobel. Mesmo que as máscaras de Prewitt sejam mais simples de implementar do que as máscaras de Sobel, as de Sobel são mais utilizadas por melhor suavização, diminuindo os ruídos [2, p. 468].

Ao calcular a magnitude como uma aproximação da soma dos valores absolutos dos componentes de gradiente \(G_x\) e \(G_y\), Equação (6.10), pode se perder a propriedade isotrópica dos filtros. No caso das máscaras de Sobel e de Prewitt, este problema não ocorre, pois dão resultados isotrópicos apenas para bordas verticais e horizontais, e que são independentes da Equação (6.9) ou Equação (6.10) [2, p. 468].

6.2.3 Método de Marr-Hildreth

Nos métodos de detecção de bordas utilizando a derivada de segunda ordem se observa maior sensibilidade aos ruídos, assim, recomenda-se um pré-processamento de suavização. A técnica de detecção proposta por Marr e Hildreth (1980), por exemplo, combina a filtragem Gaussiana com o operador Laplaciano (Figura 6.2) [3, p. 163]. Após a suavização da imagem com o filtro gaussiano, as bordas são identificadas pelos pontos de cruzamento por zero da segunda derivada.

Um aspecto que torna a técnica interessante para imagens de diferentes escalas é que considera as características da borda e dos ruídos, empregando-se operadores de tamanho mais adequado para cada imagem [2, p. 470]. Operadores de maior tamanho são recomendados para detectar bordas borradas, enquanto operadores menores detectam melhor detalhes finos com foco nítido. Como o laplaciano é isotrópico, respondendo de forma igual às variações nas diferentes direções, evita-se a utilização de várias máscaras [2, p. 472].

O operador proposto por Marr e Hildreth é obtido pela convolução, Equação (6.15) \[g(x,y) = \nabla^2[G(x,y)*f(x,y)] \tag{6.15}\] em que \(f(x,y)\) é a imagem, \(\nabla^2\) é o operador laplaciano, (\(\partial^2 f / \partial x^2 + \partial^2 f / \partial y^2\)), e \(G\) é a função gaussiana 2-D, (6.16): \[G(x,y) = e^{-\frac{x^2 + y^2}{2\sigma^2}} \tag{6.16}\] com desvio padrão \(\sigma\). Em razão da linearidade das operações, a ordem da diferenciação e da convolução podem ser alteradas [3, p. 163], assim, após a diferenciação da expressão gaussiana, obtém-se o Laplaciano da Gaussiana (LoG), Equação (6.17): \[\nabla^2G(x,y) = \begin{bmatrix} \frac{x^2 + y^2 - \sigma^2}{\sigma^4} e^{-\frac{x^2 + y^2}{2\sigma^2}} \end{bmatrix} \tag{6.17}\]

As máscaras podem ser geradas pela amostragem da Equação (6.17) com ajustes nos coeficientes para que a soma seja zero. Um exemplo de máscara 5x5 que atende ao Laplaciano da Gaussiana está na Figura 6.11(d). O comportamento dessa máscara é próximo do efeito da função LoG na Figura 6.11(a), em que o termo positivo e central é rodeado por uma região negativa cujo os valores aumentam ao se distanciar da origem, e uma região externa com zeros [2, p. 472].

Figura 6.11: (a) Gráfico 3-D do negativo de LoG. (b) Imagem do negativo de LoG. (c) Seção transversal de (a). (d) Aproximação de máscara 5x5 para LoG. [2, p. 471]

Devido ao formato na Figura 6.11, a função LoG é conhecida como operador de chapéu mexicano. Seu gráfico 3-D, sua imagem e sua seção transversal se referem ao negativo da função LoG. Na seção transversal (Figura 6.11(c)), o cruzamento por zero do LoG ocorre em \(x^2 + y^2 = 2 \sigma^2\) , definindo um círculo centrado na origem e de raio \(2\sigma\).

Na prática, o filtro LoG é gerado pelas seguintes etapas [2, p. 472]:

1. Define-se um filtro \(n\)×\(n\) gaussiano a partir de amostragem com a Equação (6.16). Lembrando da sugestão que o tamanho do filtro gaussiano, \(n\), precisa ser o menor inteiro ímpar maior ou igual a \(6\sigma\).

2. Após suavização da imagem com o filtro gaussiano, o resultado é processado pelo laplaciano, por exemplo, com uma máscara 3×3 da Figura 6.2.

3. Na imagem resultante da etapa anterior são encontrados os pontos de cruzamento por zero. Estes pontos podem ser identificados em um pixel, \(p\), com base na sua vizinhança 3x3. No caso de \(p\) ser um cruzamento por zero, pelo menos dois de seus vizinhos opostos devem apresentar sinais diferentes. Neste caso são realizados quatro testes: esquerda/direita, acima/abaixo e com as duas diagonais. Quando se utiliza um limiar para identificar o cruzamento por zero, tanto os sinais dos vizinhos opostos devem ser diferentes quanto o valor absoluto da diferença numérica deve ultrapassar o limiar para que o ponto \(p\) seja um cruzamento por zero.

O filtro LoG também pode ser aproximado com a convolução de uma máscara gerada a partir da diferença de duas funções gaussianas (DoG), Equação (6.18) [2, p. 473]: \[DoG(x,y) = \frac{1}{2\pi \sigma^2_1} e^ {-\frac{x^2+y^2}{2\sigma^2_1}} - \frac{1}{2\pi \sigma^2_2} e^ {-\frac{x^2+y^2}{2\sigma^2_2}} \tag{6.18}\]

com \(\sigma_1 > \sigma_2\). Marr e Hildreth mostraram que para \(\sigma_2/\sigma_1 = 1.6\) o operador tem maior aproximação com a função LoG [2, p. 473]. Para que LoG e DoG tenham os mesmos cruzamentos por zero se sugere que se mantenha a seguinte relação para o valor de \(\sigma\) em LoG, Equação (6.19): \[\sigma^2 = \frac{\sigma^2_1\sigma^2_2}{\sigma^2_1 - \sigma^2_2} \ln \begin{bmatrix} \frac{\sigma^2_1}{\sigma^2_2} \end{bmatrix} \tag{6.19}\]

Para estabelecer uma mesma escala de amplitude no resultado dos dois operadores, LoG e DoG, ocorre um ajuste para o mesmo valor na origem em ambas as funções [2, p. 474].

6.2.4 Método de Canny

O algoritmo de Canny recebeu esse nome em alusão a John Canny, que o propôs em seu artigo, “A computational Approach to Edge Detection” [17], publicado em 1986. Sua formulação se baseava em três pontos principais:

• Uma baixa taxa de erro, ou seja, todas as bordas presentes na imagem devem ser encontradas e não deve haver respostas espúrias.
• O segundo critério diz que as bordas detectadas devem estar bem localizadas, em outras palavras, elas devem estar o mais próximo possível das bordas verdadeiras.
• O terceiro, e último, critério diz que se deve minimizar o número de máximos locais em torno da borda verdadeira para que não sejam encontrados múltiplos pixels de borda onde deve haver somente um.

Em seu trabalho, Canny buscou encontrar soluções ótimas, matematicamente, que obedecessem os três critérios. Apesar disso, é muito difícil, ou impossível, encontrar uma solução que satisfaça completamente os objetivos descritos [2, p. 474]. Todavia é possível utilizar uma aproximação por meio de otimização numérica com as bordas em degrau em um exemplo 1-D que contenham ruído branco gaussiano para mostrar que uma boa aproximação de um ótimo detector de bordas é a primeira derivada de uma gaussiana, Equação (6.20) [2, p. 474]:

\[\frac{\mathrm{d} }{\mathrm{d} x}e^{\frac{-x^2}{2\sigma^2}} = \frac{-x}{\sigma^2}e^{\frac{-x^2}{2\sigma^2}} \tag{6.20}\]

Canny demonstrou que a utilização dessa aproximação pode ser feita com uma taxa 20% inferior à solução numérica, o que a torna, praticamente, imperceptível para muitas das aplicações [2, p. 474].

A ideia anterior foi imaginada em um aspecto 1-D, precisamos expandir esse conceito para uma generalização 2-D. Uma borda de degrau pode ser caracterizada pela sua posição, orientação e possível magnitude. Aplicar um filtro Gaussiano em uma imagem e depois diferenciá-la forma um simples e efetivo operador direcional [18, p. 145]. Digamos, então, que \(f(x,y)\) seja uma imagem e \(G(x,y)\), a função gaussiana, Equação (6.21):

\[G(x,y) = e^{-\frac{x^2+y^2}{2\sigma^2}} \tag{6.21}\]

Temos como saída a imagem suavizada, \(f_s\), Equação (6.22):

\[f_s(x,y)=G(x,y)*f(x,y) \tag{6.22}\]

E, após isso, realizamos o cálculo da magnitude, Equação (6.23), e a direção do gradiente, Equação (6.24):

\[M(x,y) = \sqrt{g_x^2+g_y^2} \tag{6.23}\] \[\alpha(x,y)= \tan^{-1}\left ( \frac{g_y}{g_x} \right ) \tag{6.24}\]

onde \(g_x=\partial f_s/\partial x\) e \(g_y=\partial f_s/\partial y\). Para o cálculo das derivadas parciais, podemos utilizar tanto Prewitt quanto Sobel.

Como essa primeira etapa utiliza operadores que calculam as primeiras derivadas, isso produz bordas grossas, e o terceiro objetivo da proposta de Canny é ter bordas com único ponto, por isso o próximo passo é o de afinar as bordas encontradas. O método que usaremos para isso é chamado supressão dos não máximos.

A etapa de não máximos tem como base a discretização das direções da normal da borda (vetor gradiente), ou seja, em uma região 3x3, temos 4 direções possíveis, como pode ser visto na Figura 6.12(c); por exemplo, uma borda de \(45º\), se ela estiver entre \(+157.5º\) e \(+112.5º\) ou \(-67.5º\) e \(-22.5º\). Na Figura 6.12(a), temos um exemplo de duas orientações que podem existir em uma borda horizontal. Na Figura 6.12(b), podemos ver a normal de uma borda horizontal e o intervalo de valores onde a direção do vetor gradiente pode existir.

Figura 6.12: Discretização das direções. (a) Borda horizontal. (b) Intervalo dos possíveis valor do ângulo normal da borda para uma borda horizontal. (c) Intervalo de valores do ângulo da normal para os diferentes tipos de borda. [2, p. 475]

Se considerarmos \(d_1\), \(d_2\), \(d_3\) e \(d_4\) como as direções possíveis em uma área 3x3, podemos formular o seguinte esquema de supressão de não máximos em todos os pontos \((x,y)\) [2, p. 475]:

• Encontrar a direção \(d_k\) que está mais perto de \(\alpha (x,y)\).

• Se o valor de \(M(x,y)\) for inferior a pelo menos um dos seus dois vizinhos ao longo de \(d_k\), deixe \(g_N(x,y)=0\) (supressão), senão deixe \(g_N(x,y)=M(x,y)\), em que \(g_N(x,y)\) é a imagem suprimida.

A última operação a ser realizada é a limiarização para se remover os pontos de falsas bordas. Aqui, usaremos a limiarização por histerese, que utiliza dois limiares, um baixo (\(T_L\)) e um alto (\(T_H\)), sendo que Canny sugeriu, em seu trabalho, que a razão entre o limiar alto e o baixo deve ser de 2:1 ou 3:1.

Podemos imaginar essa limiarização da seguinte forma, em que se cria duas imagens adicionais, (6.25) e (6.26)

\[g_{NH}(x,y) = g_N(x,y)\geq T_H \tag{6.25}\]

\[g_{NL}(x,y) = g_N(x,y)\geq T_L \tag{6.26}\]

Onde \(g_{NH}(x,y)\) e \(g_{NL}(x,y)\) são definidas inicialmente como \(0\).

Dessa forma, \(g_{NH}(x,y)\) conterá os pixels que são maiores que o nosso limiar alto e \(g_{NL}(x,y)\), os que estão acima do nosso limiar baixo, o que significa que \(g_{NL}(x,y)\) contém os pixels que estão entre os dois limiares e os que estão acima do limiar alto. A próxima etapa é remover esses pixels redundantes entre \(g_{NL}\) e \(g_{NH}\), (6.27): \[g_{NL}(x,y)=g_{NL}(x,y)-g_{NH}(x,y) \tag{6.27}\]

Sem redundância, chama-se os pixels de \(g_{NH}(x,y)\) de pixels fortes e, os de \(g_{NL}(x,y)\), de fracos. Ao final dessa limiarização, todos os pixels fortes são classificados como borda válida, mas com falhas, que nos leva a outro processo:

1. Localizar o próximo pixel de borda, \(p\), a ser revisado em \(g_{NH}(x,y)\).
2. Classificar todos os pixels fracos de \(g_{NL}(x,y)\) que tenham conexão como bordas válidas, por exemplo, os que tiverem conectividade-8.
3. Enquanto todos os pixels de \(g_{NL}(x,y)\) não forem analisados, retorna-se ao passo 1, senão continuamos ao passo 4.
4. Zerar todos os pixels de \(g_{NL}(x,y)\) que não são bordas válidas.

Ao final desses processos, teremos a imagem de saída do algoritmo de Canny. Como dito por [2, p. 476], o uso de duas imagens para \(g_{NH}(x,y)\) e \(g_{NL}(x,y)\) é uma boa maneira para se explicar o algoritmo de uma maneira simples, mas, na prática, isso pode ser feito diretamente na imagem \(g_N(x,y)\).

Finalmente, sumarizando os passos do algoritmo, com um exemplo passo-a-passo:

1. Imagem original

Figura 6.13: Imagem original.

2. Aplicação do filtro gaussiano para suavizar a imagem.

Figura 6.14: Imagem filtrada com filtro gaussiano.

3. Cálculo da magnitude do gradiente e dos ângulos.

Figura 6.15: (a) Sobel na direção vertical. (b) Sobel na direção horizontal. (c) Gradiente. (d) Ângulos. [9, p. 98]

4. Aplicação da supressão não máximos para afinar as bordas.

Figura 6.16: Resultado da supressão não máxima.

5. Usar limiarização por histerese.

Figura 6.17: Resultado da histerese.

6. Resultado final, após a análise de conectividade para detectar e conectar as bordas.

Figura 6.18: Resultado final da detecção de bordas de Canny.

6.3 Transformada de Hough

A Transformada de Hough é uma técnica utilizada para detectar formas em imagens, sejam elas linhas, círculos ou elipses, apesar de ela ser muito utilizada e ter sido criada, principalmente, para detecção de linhas.

6.3.1 Transformada de Hough para detecção de linhas

Para começar a entender essa transformada, imaginemos que temos um ponto \((x_i, y_i)\) no plano \(xy\) e a equação da reta \(y_i=ax_i+b\). É fato que pelo ponto \((x_i, y_i)\), passam infinitas retas. Podemos escrever a equação anterior em relação a \(b\), ou seja, \(b=-x_ia+y_i\), o que nos leva ao plano \(ab\) (espaço de parâmetros) onde essa nova equação gerará uma única reta.

Imaginemos um outro ponto \((x_j, y_j)\) no plano \(xy\), podemos também levá-lo ao plano \(ab\) através da equação \(b=-x_ja+y_j\). Como podemos ver na Figura 6.19(b), as duas retas geradas no plano \(ab\) se cruzam nas coordenadas \((a', b')\). O ponto de cruzamento representa a reta que cruza os dois pontos no plano \(xy\), como podemos ver na mesma representação 6.19(a). Na realidade, todos os pontos pertencentes a reta definida por esses dois pontos em \(xy\), tem sua reta respectiva em \(ab\) e todas elas se cruzam no ponto \((a', b')\), isso nos dá uma maneira de realizar a detecção de bordas, pois podemos imaginar essa reta no plano \(xy\) como nossa borda, assim, para achá-la, basta localizar o ponto no espaço de parâmetros onde um grande número de retas se cruzam.

Figura 6.19: Planos \(xy\) e \(ab\) [2, p. 483].

Ocorre um pequeno problema nessa forma, pois quando a reta se aproxima da direção vertical, \(a\), o coeficiente angular da reta, aproxima-se do infinito. Por essa razão, em vez de levarmos os pontos a retas no espaço \(ab\) cartesiano, utilizamos um espaço em coordenadas polares. Portanto, utilizamos a seguinte Equação (6.28):

\[\rho=x\cos{\theta}+y\ sen{\ \theta} \tag{6.28}\]

A Figura 6.20 mostra a aplicação de coordenadas polares nesse contexto por exemplos gráficos. Na Figura 6.20(a), \(\rho\) é a distância da origem até a reta. Na Figura 6.20(b), mostra-se que cada uma das curvas senoidais representa as infinitas retas que passam por cada um dos dois pontos, \((x_i,y_i)\) e \((x_j,y_j)\) e a interseção das curvas, \((\rho',\theta')\), é a reta que passa por esses dois pontos.

Figura 6.20: Exemplo de conversão de uma reta no plano cartesiano para o plano polar. (a) Pode ser dois pontos arbitrários de uma imagemImagem de ônibus com filtro de aguçamento e de suavização. [9, p. 98]

A Figura 6.20(c) mostra como fazemos a representação digital do espaço de coordenadas polares, usamos uma matriz onde esse espaço é subdividido em várias células, chamadas células acumuladoras. Os valores de \(\theta_{\text{min}}\) e \(\theta_{\text{max}}\) são, geralmente, \(-90^{\circ}\leq \theta\leq90^{\circ}\) e os valores de \(\rho_{min}\) e \(\rho_{max}\) são \(-D\leq\rho\leq D\), onde \(D\) é o comprimento da diagonal da imagem, ou seja, \(D=\sqrt{altura^2+largura^2}\). Essa etapa consiste em andar por todos os pontos, \((x,y)\), de borda da imagem de entrada e calcular o valor de \(\rho\), a partir da Equação (6.28), variando o ângulo \(\theta\). Com isso, a cada valor do ângulo, teremos um \(\rho\) diferente e, então, na célula acumuladora \((\rho,\theta)\) da matriz, 6.20(c), incrementa-se 1, uma espécie de voto a candidato de reta. Ao final de todo o processo, temos determinadas células com valores mais altos, conhecidas como picos, que correspondem ao cruzamento de duas ou mais curvas senoidais do plano \((\rho,\theta)\) e a uma linha que liga pontos no plano \(xy\).

A seguir temos um exemplo, que nos ajuda a entender e ver o funcionamento da transformada de Hough na prática. A Figura 6.21(a) contém uma imagem de tamanho 101x101 com um ponto no centro, ou seja, \((x,y)=(50,50)\). A Figura 6.21(b) contém a matriz acumuladora da transformada, que podemos ver a curva senoidal formada pelo ponto. Verificando os valores nela, vemos os resultados com diferentes \(\theta\):

• para \(\theta=-90^{\circ}\) \[\rho=50 \cdot \cos(-90^{\circ})+50\cdot\text{sen}(-90^{\circ}) = -50\]
• para \(\theta=90^{\circ}\) \[\rho=50\cdot \cos(90^{\circ})+50\cdot\text{sen}(90^{\circ})=50\]
• para \(\theta=45^{\circ}\) \[\rho=50\cdot \cos(45^{\circ})+50\cdot \text{sen}(45^{\circ})\approx70,71\]
• para \(\theta=-45^{\circ}\) \[\rho=50\cdot\cos(-45º)+50\cdot \text{sen}(-45º)=0\]

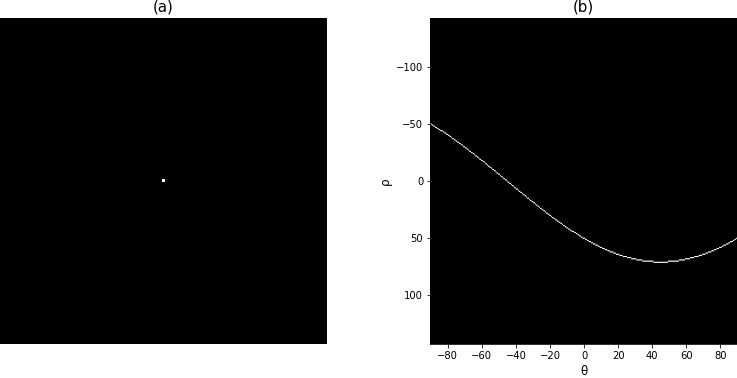
Figura 6.21: Transformada de Hough para um ponto.

Na Figura 6.22(a), temos dois pontos, \(a\) e \(b\), onde foi realizada a transformada de Hough que tem a Figura 6.22(b) como espaço de saída. A reta \(c\) que passa por esses dois pontos, representada em pontilhado na Figura 6.22(a) e, na Figura 6.22(b), temos o ponto no plano que representa essa reta, ou seja, uma reta a uma distância \(\rho\approx70,71\) da origem com o ângulo de \(45^{\circ}\).

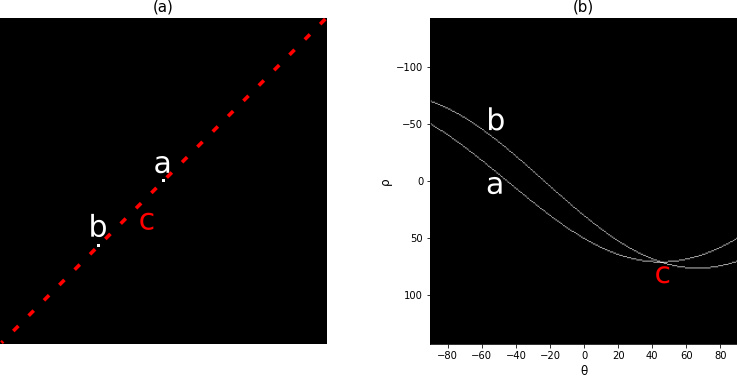
Figura 6.22: Transformada de Hough para um ponto em 45º.

Na Figura 6.23(a) temos mais um exemplo, desta vez com um ponto localizado a sua direita, diferentemente da anterior, esses dois pontos formam uma reta de \(-45^{\circ}\), fato que pode ser visto na Figura 6.23(b) onde o ponto de encontro das duas curvas acontece em \(\theta=-45^{\circ}\) com um valor de \(\rho=0\) já que a reta cruza a origem, ou seja, não possui distância em relação a ela.

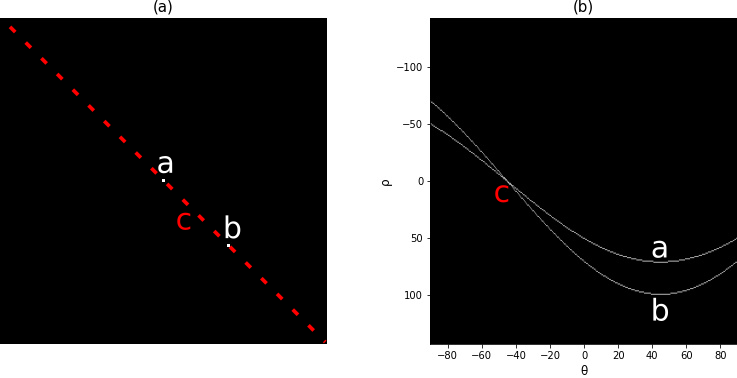
Figura 6.23: Transformada de Hough para um ponto em -45º.

Nosso último exemplo contém uma imagem com três pontos, onde temos três tipos de retas possíveis. Observando a figura 6.24(a), podemos ver os pontos \(a\), \(b\) e \(c\) e as retas \(d\), \(e\) e \(f\) que passam por eles e, na Figura 6.24(b), temos a transformada de Hough para essa imagem, algo interessante de se notar é o fato de a reta que passa pelos pontos \(b\) e \(c\) pode ser detectada duas vezes, isso se deve a uma característica da transformada de Hough chamada relação de adjacência reflexiva, ou seja, isso acontece como resultado pela maneira como \(\rho\) e \(\theta\) mudam de sinal quando chegamos as extremidades de \(\pm90^{\circ}\).

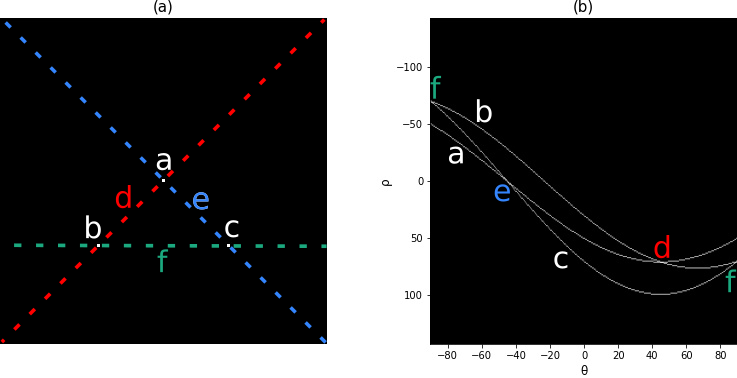
Figura 6.24: Transformada de Hough para três pontos.

Na Figura 6.25, temos nosso último exemplo na detecção de linhas, mas, desta vez, realizado em uma imagem real. Primeiramente, foi realizada a detecção de bordas pelo método de Canny, como pode ser visto na Figura 6.25(a). Logo após, foi realizada a transformação de Hough, com resultado em Figura 6.25(b) e, por fim, temos a imagem original com as linhas detectadas na Figura 6.25(c). Atenção ao fato de que nem todos os picos da transformada podem ser utilizadas como linhas, pois teríamos um número enorme delas, então utilizamos um threshold para somente as linhas que tiverem um número de votos (acumulação na matriz) superior a um valor limítrofe serem utilizadas.

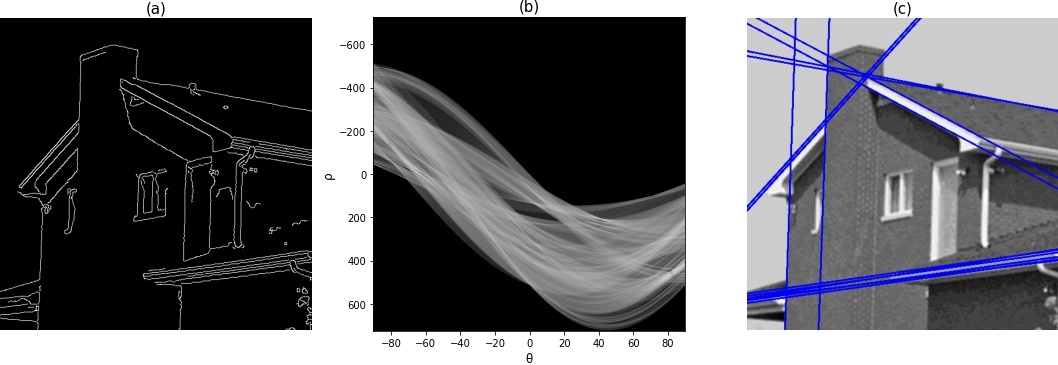
Figura 6.25: Resultado da transformada de Hough usada na detecção de linhas em uma imagem.

6.3.2 Transformada de Hough para detecção de círculos

A transformada de Hough pode ser estendida para detecção de círculos através da substituição da equação da reta pela equação do círculo (6.29): \[(x-x_0)^2+(y-y_0)^2=r^2 \tag{6.29}\]

Nesse caso, também andamos por cada pixel \((x,y)\) das bordas da imagem e o levamos ao espaço de parâmetro com as seguintes equações (6.30) e (6.31):

• \[x_0=x-r\cos(\theta) \tag{6.30}\]
• \[y_0=y-\text{sen}(\theta) \tag{6.31}\]

A diferença é que, neste caso, o nosso espaço de parâmetro terá três dimensões, porque, como desenhamos um círculo para cada pixel do círculo da imagem, a variação do diâmetro desse círculo deve levar a uma variação dos círculos descritos no espaço de parâmetros, então, também devemos variar os valores de \(r\) além dos valores de \(x\) e \(y\). Uma representação disso é vista na Figura 6.26(a), a qual temos três pixels que definem um círculo, na Figura 6.26(b), a qual temos os círculos no espaço de parâmetros, e, na Figura 6.26(c), podemos ver uma representação de um espaço de parâmetros com diferentes raios.

Figura 6.26: Transformada de Hough para círculos [19, p. 255].

A Figura 6.27 contém uma imagem com algumas moedas. Na figura 6.28(a), temos as bordas da imagem detectada com o método de Canny. Logo após, na Figura 6.28(b) - (f), temos a representação do espaço de Hough para diferentes valores de raio. E, na figura 6.29, temos o resultado da detecção de círculo após encontrados os picos do espaço de parâmetros.

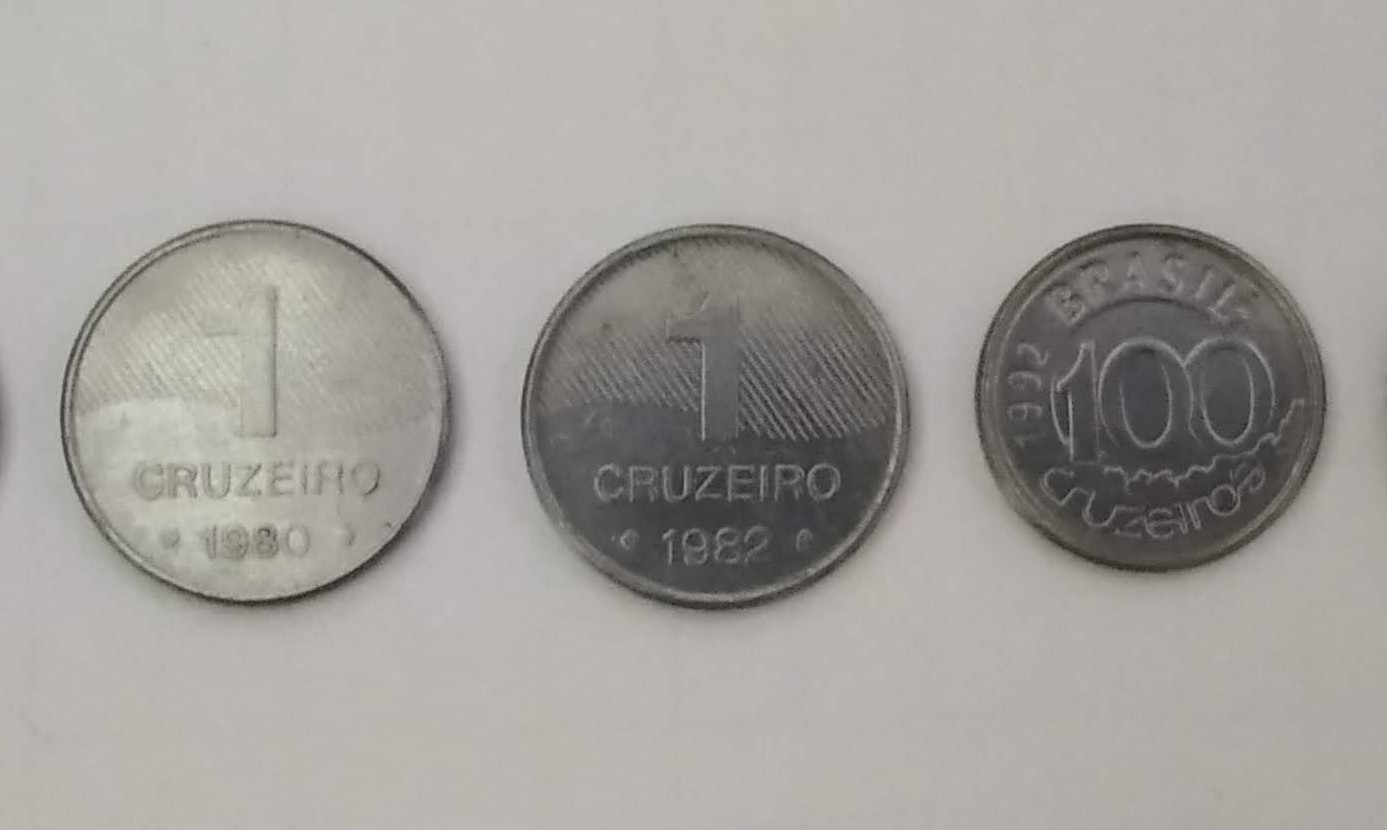
Figura 6.27: Imagem original de moedas.

Figura 6.28: Canny e espaço de parâmetros.

Figura 6.29: Resultado final da transformada de Hough para círculos.

6.4 Detecção de Quinas

Quinas são pontos chaves na visão computacional por serem muito úteis na descrição e correspondência de objetos usando poucos dados. E existem diferentes métodos para identificação dos pontos, dentre eles o mais comum é o de Harris, que é o sucessor do de Moravec [19, p. 178].

6.4.1 Detector de Quinas de Moravec

Moravec obtém sua medida de curvatura através de uma variação média de intensidade em quatro direções principais: \((0,1), (0,-1), (1,0)\) e \((-1,0)\). Isso é feito através da seguinte Equação (6.32), considerando a análise sobre o pixel \((x,y)\), o deslocamento \((u,v)\) e a janela \(2w+1\) [19, p. 185].

\[E_{u,v}(x,y) = \sum_{i=-w}^{w} \sum_{j=-w}^{w}[P_{x+i,\ y+j} - P_{x+i+u,\ y+j+v}]^2 \tag{6.32}\]

Essa equação também aproxima a função de autocorrelação na direção \((u,v)\) [19, p. 186].

O detector de Moravec apesar de ser intuitivo seu funcionamento, ele considera apenas um pequeno conjunto de mudanças possíveis. Então, Harris propôs ainda avaliar a autocorrelação, mas por uma expressão analítica [19, p. 185].

6.4.2 Detector de Quinas de Harris

O detector de Harris é desenvolvido na ideia de Moravec e sua equação, mas com uma abordagem mais complexa. Harris assume que \(P_{x+i+u,\ y+j+v}\) possa ser estimado pela série de Taylor de primeira ordem [19, p. 193]. Dessa forma (6.33),

\[P_{x+i+u,\ y+j+v} = P_{x+i,\ y+j} + \frac{\partial{P_{x+i,\ y+j}}}{\partial x}u + \frac{\partial{P_{x+i,\ y+j}}}{\partial y}v \tag{6.33}\]

Substituindo a equação anterior, (6.33), na equação de Moravec, (6.32), produz-se (6.34) \[E_{u,v}(x,y) = \sum_{i=-w}^{w} \sum_{j=-w}^{w}[\frac{\partial{P_{x+i,\ y+j}}}{\partial x}u + \frac{\partial{P_{x+i,\ y+j}}}{\partial y}v]^2 \tag{6.34}\] E expandindo a potência, (6.35) \[E_{u,v}(x,y) = A(x,y)u^2 + 2C(x,y)uv + B(x,y)v^2 \tag{6.35}\] Esta última equação pode ser representada na forma de matriz (6.36). Representação útil para compreensão mais à frente neste tópico [19, p. 187]. \[ \begin{split} E_{u,v}(x,y) &= \begin{bmatrix}u & v\end{bmatrix} \begin{bmatrix}A(x,y) & C(x,y)\\ C(x,y) & B(x,y)\end{bmatrix} \begin{bmatrix}u \\ v\end{bmatrix} \\&= D^TMD \end{split} \tag{6.36}\] onde \[A(x,y) = \sum_{i=-w}^{w} \sum_{j=-w}^{w}(\frac{\partial P_{x+i, y+j}}{\partial x})^2 \tag{6.37}\] \[B(x,y) = \sum_{i=-w}^{w} \sum_{j=-w}^{w} (\frac{\partial P_{x+i, y+j}}{\partial y})^2 \tag{6.38}\] \[C(x,y) = \sum_{i=-w}^{w} \sum_{j=-w}^{w} (\frac{\partial P_{x+i, y+j}}{\partial x})(\frac{\partial P_{x+i, y+j}}{\partial y}) \tag{6.39}\]

Como \(E_{u.v}(x,y)\) tem a forma de uma função quadrática, então possui dois eixos principais. Então, podemos rotacioná-la a fim de alinhar seus eixos com os do sistema de coordenadas, obtendo \(F_{u,v}(x,y)\), Equação (6.40) [19, p. 187]. \[F_{u,v}(x,y) = \alpha(x,y)^2u^2 + \beta(x,y)^2v^2 \tag{6.40}\]

ou em sua forma matricial (6.41). Note que são rotacionados os eixos definidos por \(D\). \[ \begin{split} F_{u,v}(x,y) &= R^TD^TMDR\\ & = D^TR^TMRD\\ & = D^TQD \end{split} \tag{6.41} \]

\[Q = \begin{bmatrix} \alpha & 0\\ 0 & \beta \end{bmatrix} \tag{6.42}\] Os valores de \(\alpha\) e \(\beta\) são proporcionais à função de autocorrelação nos principais eixos. Dessa forma, \(\alpha\) e \(\beta\) serão pequenos se o pixel \((x,y)\) for de uma região com intensidade constante, um será de valor grande e outro pequeno se estiverem em uma borda reta, e ambos terão valores grandes se estiverem em uma borda com curvatura acentuada. Portanto, a medida de curvatura em um determinado ponto é definida como \(k_k(x,y)\), (6.43) [19, p. 187]. \[k_k(x,y) = \alpha \beta - k(\alpha + \beta)^2 \tag{6.43}\] No qual \(k\) controla a sensibilidade do detector.

Como \(Q\) é uma composição ortogonal de \(M\). Os elementos de Q são chamados de autovalores [19, p. 188]. Inferimos que \[Q = R^TMR \tag{6.44}\] Então, a partir da equivalência de determinantes e traços, é possível produzir uma relação equivalente a \(Q\) com os valores da matriz \(M\), (6.45) e (6.46) [19, p. 188]. \[\alpha \beta = A(x,y)B(x,y) - C(x,y)^2 \tag{6.45}\]

\[\alpha + \beta = A(x,y) + B(x,y) \tag{6.46}\]

Assim, conforme (6.45) e (6.46), a medida de curvatura, (6.43), pode ser obtida por (6.47): \[ \begin{split} k_k(x,y) &= \alpha \beta - k(\alpha + \beta)^2 \\&= A(x,y)B(x,y) - C(x,y)^2 - k(A(x,y) + B(x,y))^2 \\&=det(M) - k(trace(M))^2 \end{split} \tag{6.47}\] A Figura 6.30(a) é a imagem original. A Figura 6.30(b) foi gerada usando o detector de Harris com uma vizinhança 5x5 (\(w=2\)) para cada deslocamento \((u,v)\), com a derivada sendo calculada pelo Operador de Sobel (3x3) e com sensibilizador \(k=0.01\). Limiarizou-se a imagem de curvatura, descartando os valores que não fossem maiores que 9% do valor máximo. E nas posições \((x,y)\) da imagem que continham as curvaturas, foi destacado em rosa. Observe que a imagem identificou as quinas do tabuleiro de xadrez e do cubo mágico, porém não detectou outras quinas como as das árvores. Além disso, foi encontrado quinas que não são próprias dos objetos, e sim da iluminação. Variando tanto o sensibilizador da função, \(k\), como o limiar é provável que consigamos encontrar mais quinas, com o custo de também poder classificar ruídos que foram identificados como bordas também como quinas. Entretanto, já vimos que o filtro gaussiano pode ser que nos ajude nesse problema.

Figura 6.30: Exemplo de detecção de Quinas pelo método de Harris.

6.5 Detecção de Blobs

Blobs, traduzido para português como bolhas, são regiões da imagem em que os pixels têm valores, aproximadamente, iguais. Uma boa representação - um tanto quanto artificial - disso é a função gaussiana, como pode ser vista sua representação 3-D, na Figura 6.31(a), e sua representação 2-D, na Figura 6.31(b), temos, em ambas, um conjunto de pixels com valores bem próximos, o que caracteriza um blob.

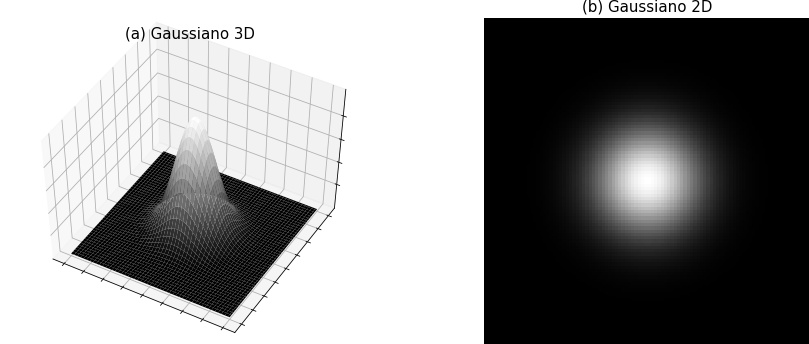
Figura 6.31: Função gaussiana em 3-D e 2-D.

Apesar do exemplo, a detecção de blobs não se restringe aos elementos circulares, mas a qualquer conjunto de pixels.

6.5.1 LoG

Esse método utiliza o Laplaciano da Gaussiana, que já foi apresentado anteriormente, mas que, resumidamente, é o cálculo de derivadas de segunda ordem em uma imagem convolucionada com um filtro gaussiano. Isso gerará fortes respostas positivas em blobs escuros e negativas em blobs claros de tamanho \(\sqrt{2\sigma}\). Como existe uma relação entre as respostas e o tamanho do \(\sigma\), é necessário realizar a operação com vários valores de \(\sigma\), pois, assim, detecta-se blobs de diferentes tamanhos.

Figura 6.32: Imagem de Campo Ultraprofundo do Hubble [20].

Como podemos ver na Figura 6.31 com diferentes valores de \(\sigma\), consegue-se detectar objetos de tamanhos variados, por exemplo, na Figura 6.33(a), detectam-se as estrelas da Figura 6.32 que apresentam uma menor resposta ao filtro laplaciano.

Figura 6.33: Laplaciano do Gaussiano com diferentes valores de sigma.

Na Figura 6.34, tem-se o resultado da detecção dos blobs utilizando LoG. Note que nem todas as estrelas foram detectadas, isso se deve ao fato do uso de um valor de threshold, o qual queremos as detecções acima de um determinado limiar. Na Figura 6.35, pode-se ver o resultado com um valor de limiar menor, onde muito mais objetos foram localizados.

Figura 6.34: Resultado da detecção de blobs com LoG.

Figura 6.35: Resultado da detecção de blobs com LoG com um threshold menor.

6.5.2 DoG

O método de DoG é, basicamente, o mesmo do anterior, mas possui uma certa vantagem, que é o fato de ele ser mais eficiente. Como também já foi mencionado no tópico na seção anterior, Marr-Hildreth, é possível aproximar o Laplaciano da Gaussiana através da Diferença de Gaussianas (DoG), ou seja, primeiramente, realiza-se a filtragem gaussiana com dois \(\sigma\) diferentes e se faz a subtração entre os dois. Realizamos esse processo para diferentes pares de valores, dessa forma, obtém-se o mesmo espaço de escala construído com o processo do LoG. Na Figura 6.36, tem-se um exemplo de detecção por DoG.

Figura 6.36: Resultado da detecção de blobs com DoG.

6.5.3 DoH

Uma matriz Hessiana é uma matriz que contém as derivadas de uma função. No nosso caso, utilizamos a Hessiana de ordem 2, pois estamos trabalhando com imagens, logo duas dimensões. Ela pode ser representada da seguinte maneira (6.48):

\[H[f(x_1, x_2, \dots,x_n)]= \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n}\\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n}\\ \vdots & \vdots & \ddots & \vdots\\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \ldots & \frac{\partial^2 f}{\partial x^2_n} \end{bmatrix} \tag{6.48}\]

A matriz Hessiana tem muita utilidade, pois ela possibilita descrever a curvatura em um ponto da função multivariável, o que, no nosso caso, pode ajudar a detectar os blobs, já que eles são aglomerados de pixels e devem estar separados do restante da imagem, ou seja, um aglomerado claro em um fundo escuro e vice-versa. Isso irá fazer com que sua função tenha uma mudança de sinal que pode ser detectada através das informações da matriz. Além disso, como dito por Herbert Bay et al.[21], os detectores baseados na Hessiana são mais estáveis e repetíveis (tem a mesma resposta para a mesma imagem com diferentes ângulos, iluminações etc.).

Um dos principais algoritmos que fazem uso dessa matriz se chama Speeded Up Robust Features (SURF)[21]. Esse método faz uso de várias técnicas que o tornam muito rápido, como seu próprio nome sugere. Uma dessas técnicas é o cálculo da integral da imagem, realizado a partir da soma de todos os pixels de uma área retangular a partir do \(x\) atual, sendo que este varia a medida que se anda pela imagem.

Figura 6.37: Integral de uma imagem [22].

Como pode ser visto na Figura 6.37, a integral de uma imagem contém a soma das regiões, por exemplo, a primeira posição contém a soma de somente uma célula, no caso \(1\). A segunda posição tem a soma de duas células. Note que, na primeira linha, está, basicamente, somando as células de uma só linha. Na segunda linha, começa-se a formar regiões retangulares, por exemplo, na segunda linha e na terceira coluna há o valor \(6\), resultante da soma das seis células da primeira linha com a segunda. Com a integral, pode-se calcular a área de qualquer região com apenas quatro operações, da seguinte forma, (6.49): \[soma = D+A-B-C \tag{6.49}\]

onde \({A,B,C,D}\) formam uma região, como exemplo, o cálculo da área 2x2 no canto inferior direito da Figura 6.37, (6.50): \[soma = 9 + 1 - 3 - 3 = 4 \tag{6.50}\]

Isso nos ajuda na aplicação de box filters, já que precisaríamos da soma de determinadas áreas, porque, com isso, aumentamos a velocidade do método. Sendo \(X=(x,y)\) um ponto em uma imagem, sua matriz Hessiana em \(X\) a uma escala \(\sigma\) é dada por:

\[H(X,\sigma)=\begin{bmatrix} L_{xx}(X, \sigma) & L_{xy}(X, \sigma)\\ L_{xy}(X, \sigma) & L_{yy}(X, \sigma) \end{bmatrix} \tag{6.51}\]

onde \(L_{xx}(X, \sigma)\) é a convolução da imagem no ponto \(X\) com a derivada de segunda ordem gaussiana \(\frac{\partial^2g(\sigma)}{\partial x^2}\) e assim por diante [21]. Aqui, entra em cena mais um elemento para melhorar a velocidade do algoritmo, Bay, Herbert et al. utilizam box filters para aproximar o filtro gaussiano. Como podemos ver, na Figura 6.38, os dois primeiros filtros são os derivativos gaussianos discretizados e os dois últimos são os aproximados a partir de box filters.

Figura 6.38: Filtro gaussiano discretizado e aproximado nas direções \(y\) e \(xy\) [21].

Chamamos as derivadas realizadas na imagem de \(D_{xx}\), \(D_{yy}\), \(D_{xy}\). Essas derivadas não são realizadas com somente um valor de \(\sigma\), seguem o mesmo raciocínio que os detectores anteriores, usam uma sequência de valores para, assim, criar um espaço de escalas e conseguir detectar blobs de diferentes tamanhos.

A determinante da Hessiana é dada por (6.52):

\[det(H_{\text{aprox}}) = D_{xx}D_{yy}-(0.9D_{xy})^2 \tag{6.52}\]

O valor \(0.9\) é um peso introduzido pelos autores Bay, Hebert et al. para corrigir as respostas quando utilizamos várias escalas de sigma e obter uma invariância escalar. Na Figura 6.39, tem-se o resultado de uma detecção de blobs realizada pela Determinante do Hessiano.

Figura 6.39: Resultado da detecção de blobs com DoH.

6.6 Limiarização

A limiarização, como próprio nome sugere, é um ou mais limiares, valores limites, que são responsáveis por segmentar uma imagem em regiões com base nos valores de intensidade e/ou propriedades desses valores [2, p. 486]. Sua boa repercursão dada em segmentações de imagem é por sua simplicidade de implementação, velocidade computacional e propriedades intuitivas [2, p. 486].

É importante salientar que a chance de sucesso da limiarização de intensidade é proporcional à largura e à profundidade do(s) vale(s) que separam os modos (ou classes) do histograma. E os principais fatores que afetam as propriedades do(s) vale(s) são [2, p. 487]:

• A separação entre picos: quanto mais distantes forem os picos entre si, melhores as possibilidades de separação da imagem;

• Índice de ruído da imagem: os modos ficam mais largos com o aumento do ruído;

• O tamanho relativo dos objetos e do fundo;

• A uniformidade da fonte de iluminação;

• A uniformidade da reflexão da imagem.

Suponha os histogramas de intensidade de duas imagens composta por objetos claros sobre um fundo escuro, conforme Figura 6.40, de tal forma que os pixels de seus objetos e do fundo tenham valores de intensidade agrupados em modos (ou grupos, ou classes), para segmentar as regiões da imagem, que também pode ser visto como segmentar os modos do histograma, devem ser encontrados os limiares entre os modos capazes de ter a melhor segmentação². Então, no histograma da Figura 6.40(a), usa-se um limiar, pois há um vale bem definido, já na Figura 6.40(b), há dois vales, logo é possível usar dois limiares para segmentar as regiões da imagem.

A segmentação do objeto claro da imagem que possui o histograma da Figura 6.40(a) é dada por \(g(x,y)\), sua imagem de saída:

\[g(x,y) = \begin{cases} 1,\ se\ f(x,y) > T \\ 0,\ se\ f(x,y) \leq T \end{cases} \tag{6.53}\]

Note que se cria uma binarização, uma imagem preta e branca, que pode ser vista como uma máscara a ser aplicada na imagem do histograma, multiplicando a imagem pela máscara. E, analogamente ao caso anterior, após definido os limiares de uma imagem com mais modos, por exemplo, numa imagem com três modos, as regiões poderiam ser identificadas pelas cores branca, cinza e preta.

Figura 6.40: Histogramas de intensidade que podem ser divididos por um limiar único, (a), e limiares duplos, (b). [2, p. 486]

Quando \(T\) é uma constante aplicável em uma imagem inteira, o processo é conhecido como limiarização global. Caso \(T\) mude ao longo da imagem, usamos o termo limiarização variável. E quando \(T\) denotar uma limiarização variável na qual o valor \(T\) em qualquer ponto \((x,y)\) em uma imagem depende das propriedades de sua vizinhança, por exemplo, a intensidade média dos pixels da vizinhança, o chamamos de limiarização local ou regional³ [2, p. 486].

Os problemas de segmentação que exigem mais do que dois limiares são difíceis (muitas vezes impossíveis) de se resolver e seus melhores resultados, geralmente, são obtidos através dos métodos como a limiarização variável ou aumento da região [2, p. 486].

• O papel do ruído da limiarização

O ruído de uma imagem é capaz de fazer com que fique difícil achar um limiar ideal para segmentar a imagem sem processamentos adicionais, pois o(s) vale(s) da imagem podem desaparecer [2, p. 487].

Observe que, conforme os exemplos da Figura 6.41 e seus respectivos histogramas, o aumento no desvio padrão nos níveis de intensidade do ruído gaussiano faz com que o vale que separava os dois modos desapareça, o que torna difícil a segmentação do fundo e do objeto.

Figura 6.41: (a) Imagem de 8 bits livre de ruído, produção típica de uma Computação Gráfica. (b) Imagem com ruído gaussiano aditivo com \(\mu = 0\) e \(\sigma\) de 10 níveis de intensidade. (c) Imagem com ruído gaussiano aditivo com \(\mu = 0\) e \(\sigma\) de 50 níveis de intensidade. (d) a (f) Histogramas correspondentes [2, p. 487].

• O papel da iluminação e refletância

O problema da iluminação é quando não é possível ter uma incidência uniforme de luz, causando um sombreamento. O mesmo efeito acontece quando o problema não é na iluminação, mas nas características da superfície do objeto; pois a iluminação e refletância produzem problemas equivalentes. Note que, pela Figura 6.42, o histograma deixou de ser bimodal. Logo não é simples de segmentar imagens com problemas de iluminação e refletância.

Figura 6.42: (a) é a imagem ruidosa. (b) é a rampa de intensidade no intervalo \([0.2, 0.6]\). (c) é o produto de (a) e (b). (d) a (f) são os histogramas correspondentes [2, p. 488].

Há três abordagens básicas para se resolver os problemas de iluminação e refletância para uma boa segmentação. Corrigir diretamente o padrão de sombreamento através de uma multiplicação com o comportamento inverso do sombreamento, por exemplo, uma iluminação não uniforme, porém fixa, como a da Figura 6.42, pode ser corrigida multiplicando a imagem pelo inverso do padrão de iluminação, que pode ser obtida na aquisição de uma imagem de uma superfície plana de intensidade constante. Outra alternativa é corrigí-lo por meio do processamento, por exemplo, utilizando a transformada top-hat. E a terceira abordagem é a de contornar isso utilizando a limiarização variável [2, p. 488].

6.6.1 Limiarização Global Simples

A limiarização global simples é um método iterativo básico e que não é o mais eficiente. Ele é um processo iterativo que denomina o limiar ideal como aquele que produz menor diferença entre as médias de intensidade dos modos, o segmentado e o desprezado [2, p. 488].

Ele consiste em:

1. Selecionar uma estimativa inicial para o limiar global, \(T\).

2. Segmentar a imagem usando \(T\). Isso dará origem a dois grupos de pixels: \(G_{1}\), composto por todos os pixels com valores de intensidade \(> T\), e \(G_{2}\), composto pelos pixels com valores \(\leq T\).

3. Calcular os valores de intensidade média dos grupos: \(m_{1}\) e \(m_{2}\).

4. Calcular um novo valor de limiar: \(T = \frac{m_{1}+m_{2}}{2}\).

5. Repita as Etapas 2 a 4 até que a diferença entre os valores de \(T\), com a iterações sucessiva e a atual, seja menor que o parâmetro predefinido \(\Delta T\).

A Figura 6.43 mostra um exemplo da aplicação de Limiarização Global Simples. A Figura 6.43(a) é a imagem de uma digital com ruído. A Figura 6.43(b) mostra que seu histograma possui um vale bem nítido e, pela aplicação do algoritmo, que usa \(\Delta T = 0\) e inicia \(T\) como a média de intensidade da imagem, após três iterações, encontra-se o limiar \(T = 125.4\). A Figura 6.43(c) mostra a digital segmentada pelo limiar encontrado, \(T = 125\); como esperado, pelo nítido vale, foi satisfatório o resultado.

Figura 6.43: (a) Impressão digital ruidosa. (b) Histograma. (c) Segmentação resultante usando um limiar global. [2, p. 489]

6.6.2 Limiarização pelo Método de Otsu

O método de Otsu é um método estatístico que produz o chamado limiar ótimo a partir do histograma. O limiar ótimo é denotado por aquele que maximiza a variância entre classes ou minimiza a variância intraclasse [2, p. 489].

O primeiro passo é obter o histograma da imagem normalizado, isto é, no qual os pesos de cada intensidade são a probabilidade da ocorrência daquela intensidade na imagem. Segue abaixo a Equação (6.54) que representa um histograma normalizado, no qual \(L\) representa a quantidade de níveis de intensidade e \(p_{i}\), a probabilidade de ocorrência da intensidade \(i\) na imagem [2, p. 490].

\[\sum_{i=0}^{L-1}{p_{i} = 1,\ p_{i} \geq 0} \tag{6.54}\]

Para entender a equação principal de Otsu, Equação (6.58), precisa-se compreender algumas equações que a compõe. A probabilidade de ocorrência do modo \(1\) é dada pela Equação (6.55) [2, p. 490]: \[P_{1}(k) = \sum_{i=0}^{k}{p_{i}} \tag{6.55}\]

E o valor da intensidade média dos pixels da classe \(1\), \(C_{1}\), para dado limiar \(k\) pode ser calculado pela Equação (6.56) [2, p. 490]

\[\begin{split} m_{1}(k) & = \sum_{i=0}^{k}{iP(i/C_{1})}\\ & = \sum_{i=0}^{k}{iP(C_{1}/i)P(i)/P(C_{i})}\\ & = \frac{1}{P_{1}(k)}\sum_{i=0}^{k}{ip_{i}}\\ \end{split} \tag{6.56}\]

E a média acumulada (intensidade média) até o nível \(k\) ou da classe \(C_{1}\) é dada pela Equação (6.57) [2, p. 490]: \[m(k) = \sum_{i=0}^{k}{ip_{i}} \tag{6.57}\]

Entendidas as equações anteriores, chegamos a equação principal, Equação (6.58), que denota a variância entre classes. \[\sigma_B^2(k) = \frac{[m_GP_{1}(k) - m(k)]^{2}}{P_1(k)[1 - P_1(k)]} \tag{6.58}\]

Então, o limiar ótimo é o valor que maximiza a variância entre classes, denominado \(k^*\), demonstrado pela Equação (6.59) [2, p. 491]. E conforme informado anteriormente, esse resultado é o mesmo que minimiza a variância dentro das classes; isso se deve a uma propriedade estatística que relaciona a variância global da intensidade da imagem, a variância interclasse e a variância intraclasse. \[\sigma_B^2(k^*) = \max_{0 \leq k \leq L-1} \sigma_B^2(k) \tag{6.59}\]

Se a máxima variância entre classes existir para mais de um valor, é habitual se calcular a média desses valores \(k\) [2, p. 491].

Uma métrica adimensional, \(\eta\), pode ser usada para obter uma estimativa quantitativa da separabilidade das classes, o que dá uma idéia da facilidade de segmentação e do resultado esperado. Seu cálculo é demonstrado na seguinte Equação (6.60). Para o cálculo de \(\eta\), é necessário conhecer a variância global da intensidades da imagem, que pode ser calculada por (6.61).

\[\eta = \frac{\sigma_B^2(k^*)}{\sigma_G^2} \tag{6.60}\]

\[\sigma_G^2 = \sum_{i=0}^{L-1}{(i - m_G)}^2p_i \tag{6.61}\]

Tendo o limiar ótimo, \(k^*\), segmentamos a imagem como já visto na introdução desta seção, Limiarização.

Resumo do algoritmo de Otsu [2, p. 492]:

1. Calcular o histograma normalizado da imagem de entrada. Designar os componentes do histograma como \(p_i, i = 0, 1, 2, ..., L-1\);
2. Calcular as somas acumuladas, \(P_1(k)\), para \(k = 0, 1, 2, ..., L-1\);
3. Calcular as médias acumuladas \(m(k)\), para \(k = 0, 1, 2, ..., L-1\);
4. Calcular a intensidade média global, \(m_G\);
5. Calcular a variância entre classes, \(\sigma_B^2(k)\), para \(k = 0, 1, 2, ..., L-1\);
6. Obter o limiar ideal de Otsu, \(k^*\), caso haja mais de um, faz-se a média dos valores;
7. Obter a medida de separabilidade, \(\eta^*\), a fim de estimar a qualidade da segmentação.

A Figura 6.44(a) mostra uma imagem de microscópio ótico de células polimerosomas e a Figura 6.44(b), seu histograma. O objetivo deste exemplo é segmentar as moléculas do fundo. A Figura 6.44(c) é o resultado pela limiarização global simples. Como o histograma não tem vales distintos e a diferença de intensidade entre o fundo e os objetos é pequena, o algoritmo não conseguiu alcançar a segmentação desejada. A Figura 6.44(d) mostra o resultado obtido pelo método de Otsu. Esse resultado, obviamente, é superior ao da Figura 6.44(c). O valor do limiar calculado pelo algoritmo simples foi o de \(169\), enquanto o limiar calculado pelo método de Otsu era o de \(181\), que está mais próximo das áreas mais claras da imagem que define as células. A medida de separabilidade \(\eta\) foi \(0.467\).

Figura 6.44: (a) Imagem original. (b) Histograma (os picos elevados foram cortados para realçar os detalhes nos valores mais baixos). (c) Resultado da segmentação pela limiarização global simples. (d) Resultado da segmentação pelo método de Otsu. [2, p. 492]

6.6.3 Uso de suavização para limiarização

O objetivo da suavização é tentar separar os histogramas de imagens ruidosas, que tendem a ser unimodais, em modos com vales mais profundos; pois, quanto mais profundo o vale, melhor será a segmentação da imagem.

Atente-se ao tipo de média e ao tamanho do kernel, aconselha-se o filtro gaussiano, pois ele minimiza o borramento de fronteira, e suaviza o ruído ainda que de maneira mais branda do que um filtro de média.

A Figura 6.45(a) mostra uma imagem ruidosa, a Figura 6.45(b) mostra seu histograma, a Figura 6.45(c) mostra o resultado do método de Otsu. Já a Figura 6.45(d) mostra a imagem da Figura 6.45(a) suavizada usando uma máscara de média de tamanho 5x5 e a Figura 6.45(e) é seu histograma e a Figura 6.45(f) é resultado da limiarização pelo método de Otsu.

Figura 6.45: Exemplo de suavização antes da aplicação do método de Otsu [2, p. 493].

Apesar do filtro de média poder nos ajudar, nem sempre será capaz disso. A Figura 6.46(a) mostra uma imagem ruidosa e a Figura 6.46(b) mostra o seu histograma, observe que o pontinho branco parece nem estar presente no histograma. E após aplicado o método de Otsu, a Figura 6.46(c), observe que não foi obtida a segmentação desejada. Então, tentou-se um filtro de média 5x5, que reduz o ruído, Figura 6.46(d). O resultado no histograma foi a redução do espalhamento do histograma, Figura 6.46(e), mas a distribuição ainda é unimodal, resultando em falha na segmentação, o que é visto na Figura 6.46(f).

Figura 6.46: Exemplo de insucesso na segmentação por Otsu, mesmo com prévia suavização [2, p. 493].

Portanto, note que, se a região que deseja segmentar for muito pequena em relação ao background e houver ruído, o que pode surgir na captura da imagem, a chance de não dar certo pelos métodos vistos é grande; pois, como os métodos que até agora vimos operam apenas no histograma da imagem, sem uso de maiores recursos. Como visto, imagens com essa característica, um mínimo ruído persiste e nem foi obtido um vale considerável entre as duas regiões. Isso pode ser atribuído ao fato de que a região é tão pequena que sua contribuição para o histograma é insignificante em comparação à intensidade da propagação causada pelo ruído [2, p. 493]. A solução para isso é o uso de máscaras de borda, que será detalhado a seguir.

6.6.4 Uso de bordas para limiarização

Em uma imagem com ruído na qual a região a ser segmentada é muito pequena, é como se não houvesse aquela região e houvesse apenas o background. Isso é observado na aparência unimodal do histograma.

Portanto, fica difícil estimar um limiar ideal pelos algoritmos supracitados. E, como visto anteriormente, é preciso uma aparência bimodal para uma boa segmentação, então, precisamos de um histograma equilibrado; para isso, tomamos o histograma das bordas mais destacadas da imagem. Isso pode ser resumido em gerar uma máscara de gradiente ou laplaciano da imagem, limiarizá-la com um valor alto e usar como máscara para imagem original e prosseguir com o processo de segmentação do objeto a partir dessa amostra, pois, dessa forma, é gerado um histograma simétrico e com um vale destacado, porque, com a máscara de borda, a probabilidade de um píxel estar no background ou foreground tende a ser equilibrada [2, p. 494].

O que se espera com os tipos de máscaras de borda, conforme visto no estudo detecção de bordas, é que a de gradiente produzirá bordas mais grossas e menor detecção aos ruídos da imagem, e a de laplace, bordas mais finas e maior detecção de ruídos, além de apresentar melhor custo computacional. Entretanto, é possível modificar este algoritmo para que tanto a magnitude do gradiente quanto o valor absoluto das imagens laplacianas sejam utilizadas; nesse caso, poderíamos especificar um limiar para cada imagem e formar a lógica OU dos dois resultados para obter a imagem marcadora, essa abordagem é útil quando se deseja ter mais controle sobre os pontos que foram considerados como sendo pontos válidos de borda [2, p. 494].

Resumo das etapas de segmentação pela identificação de bordas do objeto [2, p. 494]:

1. Calcular uma imagem de borda da imagem capturada, \(f(x,y)\), ora como a magnitude do gradiente, ora como o valor absoluto do laplaciano, usando qualquer um dos métodos;

2. Especificar um valor de limiar, \(T\);

3. Limiarizar a imagem a partir da Etapa 1, utilizando o limiar estabelecido na Etapa 2 para produzir uma imagem binária, \(g_{T}(x,y)\). Esta imagem é usada como uma imagem de máscara na etapa seguinte para selecionar os pixels de \(f(x,y)\) que correspondem aos pixels “fortes” da borda;

4. Calcular um histograma utilizando apenas os pixels de \(f(x,y)\), que correspondem aos endereços de pixel avaliados com o número \(1\) em \(g_{T}(x,y)\);

5. Use o histograma da Etapa 4 para segmentar \(f(x,y)\) globalmente, utilizando, por exemplo, o método de Otsu.

A Figura 6.47(a) e (b) mostram as mesmas imagens da Figura 6.46 e seu histograma. Vimos que essa imagem não adianta ser suavizada. Entretanto, usamos a estratégia de máscara de borda que obteve um ótimo resultado. A Figura 6.47(c) mostra o gradiente já limiarizado, A Figura 6.47(d) e (e) mostra a máscara multiplicada a imagem original, que tem um histograma mais relevante à segmentação. E a Figura 6.47(f) mostra o resultado da segmentação pelo novo histograma, 6.47(e), através do Método de Otsu. O limiar foi de \(134\), que fica aproximadamente a meio caminho entre os picos no histograma.

Figura 6.47: Exemplo de limiarização por meio da máscara de borda do gradiente [2, p. 495].

Já a Figura 6.48(a) e (b) mostra uma imagem de 8 bits de células de levedura e seu histograma. A tentativa em detectar em segmentar os pontos claros pelo método de Otsu sem prévia etapa não foi sucedida, embora o método seja capaz de isolar algumas das regiões das células muitas da regiões segmentadas à direita não estão separadas. O limiar calculado foi de \(42\) e a medida de separabilidade foi de \(0.636\).
A Figura 6.48 (d) mostra a imagem \(g_T(x,y)\) obtida pelo cálculo do valor absoluto da imagem laplaciana e a limiarização com \(T\) definido a \(115\) em uma escala de intensidade no intervalo \([0, 255]\). Este valor de \(T\) corresponde aproximadamente ao percentil \(99.5\) dos valores da imagem laplaciana absoluta; assim, a limiarização a este nível deve resultar em um conjunto de pixels reduzido, como mostra esta Figura. A Figura 6.48 (e) é o histograma dos pixels diferentes a zero no produto de (a) e (d). Finalmente a Figura 6.48 (f) mostra o resultado da segmentação global da imagem original utilizando o método de Otsu baseado no histograma da Figura 6.48 (e). Este resultado está de acordo com as localizações dos pontos claros na imagem. O limiar calculado pelo método de Otsu foi \(115\) e a medida de separabilidade foi de \(0.762\), sendo que ambos são superiores aos valores obtidos utilizando o histograma original [2, p. 495].

Figura 6.48: Exemplo de limiarização por meio da máscara de borda laplaciana [2, p. 496].

6.6.5 Limiares Múltiplos

A diferença entre os limiares múltiplos e o que vimos até agora é que se usa mais de um limiar para segmentar a imagem a fim de produzir uma melhor medida de separabilidade entre as classes, por conseguinte, melhor segmentação. Entretanto, como as aplicações que requerem mais de dois limiares, geralmente, são resolvidas com mais do que apenas valores de intensidade. Ao invés disso, o caminho é usar descritores adicionais (por exemplo, cor) e o problema é moldado para reconhecimento de padrões, como explicado a seguir em limiarização baseada em diversas variáveis [2, p. 497].

No caso das classes \(K, C_1, C_2, ..., C_K\), a variância entre classes se generaliza pela expressão (6.62) \[\sigma_{B}^{2} = \sum_{k=1}^K{P_k(m_k-m_G)^2} \tag{6.62}\] na qual \[P_k = \sum_{i\in C_k}{p_i} \tag{6.63}\] \[m_k = \frac{1}{P_k} \sum_{i \in C_k}{ip_i} \tag{6.64}\] As classes \(K\) são separadas por \(K-1\) limiares cujos valores, \(k^*_1, k^*_2, ..., k^*_k-1\): \[ \sigma_{B}^{2}(k^*_1, k^*_2, ..., k^*_{K-1}) = \max_{0<k_1<k_2<...k_{n-1}<L-1}{\sigma_{B}^{2}(k_1, k_2, ..., k_{K-1})} \tag{6.65}\]

Como observado na Equação (6.65), o valor máximo é obtido por testes com todas as possibilidades de valores para cada limiar, mas não faz sentido assumir limiares para \(0\) e \(L-1\), pois são os extremos da faixa de intensidade.

Também pode ser feito a avaliação de sua medida de separabilidade, Equação (6.66). Como exemplo, tomemos um histograma com três classes. [2, p. 497]

\[\eta(k^*_1, k^*_2) = \frac{\sigma^2_{B}(k^*_1,k^*_2)}{\sigma^2_{G}} \tag{6.66}\]

A Figura 6.49(a) mostra a imagem de um iceberg. É notório que será possível dividí-la com dois limiares⁴ a partir das predominâncias de três grupos de intensidade. Olhando no histograma, 6.49(b), pelos vales bem destacados também é observado isso. Encontra-se pelo método de Otsu dois limiares, \(80\) e \(177\), com uma excelente medida de separabilidade de \(0.954\). Limiarizando a Figura 6.49(a) o resultado que se obtém é uma segmentação muito boa, Figura 6.49(c) [2, p. 498].

Figura 6.49: (a) Imagem de um iceberg. (b) Histograma. (c) Imagem segmentada em três regiões usando os limiares duplos de Otsu. [2, p. 496]

6.6.6 Limiarização variável

Vimos perante subseções anteriores, que fatores como ruído e iluminação são impecílios para uma boa segmentação. Também foi visto que suavização e informações das bordas podem ser usadas para resolver isto. No entanto, é frequente o caso que essas estratégias são ineficientes ou nem possíveis. Como solução para tal, usamos limiares variáveis.

6.6.6.1 Particionamento da imagem

O particionamento da imagem consiste em fracionar a imagem em retângulos suficientemente pequenos de maneira que eles tenham iluminação e refletância uniformes e aplicar o método de Otsu em cada um deles. O sucesso do método é análogo ao da máscara de bordas, ele produz, para cada fração, histogramas simétricos com vales profundos [2, p. 498].

A Figura 6.50(a) e (b) mostra uma imagem e seu histograma. Pelo seu histograma é plausível que não resultaria em uma boa segmentação, seja pelo método de Otsu, Figura 6.50(c) ou pelo método iterativo, Figura 6.50(d). Após fracionada a imagem, Figura 6.50(e), a segmentação por Otsu teve sucesso, Figura 6.50(f). [2, p. 498]

Figura 6.50: Exemplo da técnica de particionamento da imagem [2, p. 498].

Figura 6.51: Representa o histograma das subimagens da Figura 6.50(e) [2, p. 498].

6.6.6.2 Limiarização variável baseada nas propriedades locais da imagem

A limiarização variável baseada nas propriedades locais da imagem é uma técnica em que se calcula um limiar para cada ponto, \((x,y)\), com base em uma ou mais propriedades calculadas em sua vizinhança. Apesar disso parecer trabalhoso, os algoritmos e hardwares modernos permitem o processamento rápido da vizinhança, especialmente para as funções comuns, como as operações lógicas e aritméticas [2, p. 499]. Utilizaremos como abordagem básica duas propriedades, \(\sigma_{xy}(x,y)\) e \(m_{xy}(x,y)\), já que indicam o grau de contraste e intensidade média na vizinhança.

Seguem cálculos da limiarização usando apenas a intensidade do ponto, sendo \(T_{xy}\), o limiar local. As equações seguintes, (6.67) e (6.68) são formas comuns de limiares variáveis locais [2, p. 499]:

\[T_{xy} = a\sigma_{xy} + bm_{xy} \tag{6.67}\] em que \(a\) e \(b\) são constantes não negativas, e \[T_{xy} = a\sigma_{xy} + bm_{G} \tag{6.68}\] na qual \(m_G\) é a média global da imagem.

Também pode ser usado predicados a fim de determinar o limiar, \(T_{xy}\), de segmentação. No entanto, o preço dessa limiarização mais rebuscada é um aumento no custo computacional [2, p. 499]. E a imagem de saída, \(g_{xy}\), pode ser representada como a Equação (6.69):

\[g(x,y) = \begin{cases} 1,\ se\ f(x,y) > a\sigma_{xy}\ \ E\ \ f(x,y) > bm_{xy}\\ 0,\ caso\ contrário \end{cases} \tag{6.69}\]

A Figura 6.52(a) é a imagem de células de levedura da Figura anterior 6.48(a). A Figura 6.52(b) é um exemplo da segmentação da Figura 6.52(a) com dois limiares. Entretanto, note que as células do canto superior direito foram segmentadas de forma unida. A Figura 6.52(c) é a imagem dos desvios padrão locais da vizinhança de tamanho 3x3 de cada píxel. E foi escolhida a média global ao invés da local, pois geralmente produz melhores resultados quando o fundo é quase constante e todas as intensidades de objeto estão acima ou abaixo da intensidade do fundo. Os pesos \(a=30\) e \(b=1.5\) foram assumidos. E, por fim, foi limiarizada pelo predicado exemplificado na Equação (6.68) e não pela intensidade de um ponto, Figura 6.52(d).

Figura 6.52: Exemplo de limiarização variável baseada nas propriedades locais [2, p. 500].

6.6.6.3 Usando média de movimento

O método de médias móveis é usado geralmente quando os objetos de interesse são pequenos (ou finos) em relação ao tamanho da imagem, uma condição que as imagens de texto digitado ou manuscrito possuem [2, p. 501]. Segundo Gonzalez, essa aplicação é muito útil no processamento de documentos [2, p. 500]. O procedimento consiste em um kernel 1D que percorre a imagem linha por linha e calcula média móvel com base em um intervalo de um dado tamanho fixo. A regra inicial é usar um intervalo de tamanho cinco vezes maior que a largura média do objeto que deseja limiarizar [2, p. 501].

Digamos que \(z_{k+1}\) denota a intensidade do ponto encontrado na sequência de digitalização na Etapa \(k+1\). A média móvel (intensidade média) com este novo ponto é dada pela Equação (6.70) \[\begin{split} m(k+1) & = \frac{1}{n} \sum_{i = k+2-n}^{k+1}{z_i}\\ & = m(k) + \frac{1}{n}(z_{k+1} - z_{k-n}) \end{split} \tag{6.70}\]

na qual \(n\) é o tamanho do intervalo ou número de pixels utilizados no cálculo da média e \(m(1)=\frac{z_1}{n}\). Este valor inicial não é rigorosamente correto porque a média de um único ponto é o valor do ponto em si. No entanto, o usamos para que cálculos especiais não sejam necessários quando é executada pela primeira vez. Já que a média móvel é calculada para cada ponto da imagem, a segmentação é baseada no limiar \(T_{xy}=bm_{xy}\), em que \(b\) é constante e \(m_{xy}\) é a média móvel no ponto \((x,y)\) na imagem de entrada [2, p. 500]. A diferença desse método ao explicado anteriormente, limiarização variável baseada nas propriedades locais da imagem^(limiarização-variável-baseada-nas-propriedades-locais-da-imagem), é que, neste, usa-se um kernel 1D que avalia linha por linha da imagem pegando amostras de uma certa quantidade de pixels, na qual, conforme mencionado anteriormente neste tópico, a quantidade de pixels tem que ser cinco vezes mais larga que a largura do objeto que se deseja segmentar.

Na Figura 6.53(a) mostra uma imagem de texto escrito à mão sombreada por um padrão de intensidade. Esta forma de sombreamento de intensidade é típica de imagens obtidas com um flash fotográfico. A Figura 6.53(b) é o resultado da segmentação pela limiarização global de Otsu. A Figura 6.53(b) mostra uma segmentação bem sucedida com limiarização local usando médias móveis, usando \(n=20\), já que a largura média do traço era de \(4\) pixels, e \(b=0.5\).

Figura 6.53: Exemplo de aplicação da limiarização por médias móveis em um documento corrompido por um sombreamento típico de flash fotográfico. (a) Imagem original. (b) Aplicado método de Otsu. (c) Aplicado método de médias móveis. [2, p. 501].

Já na Figura 6.54(a) mostra uma imagem de texto escrito à mão corrompida por um sombreamento senoidal. Esta forma de sombreamento de intensidade é típica de quando o fornecimento de energia em um digitalizador de documentos não é apropriado. A Figura 6.54(a) é a imagem original, a Figura 6.54(b) é o resultado da limiarização por Otsu e a Figura 6.54(c) é o resultado pela média móvel. Os parâmetros utilizados foram o mesmo do anterior, sendo \(n=20\) e \(b=0.5\), o que mostra relativa robustez do método.

Figura 6.54: Exemplo de aplicação da limiarização por médias móveis em um documento corrompido por um sombreamento típico de problemas em scanner em que o fornecimento de energia não é o apropriado. (a) Imagem original. (b) Imagem original aplicado o método de Otsu. (c) Imagem original aplicado método de médias móveis. [2, p. 502].

6.6.7 Limiarização baseada em diversas variáveis

Até agora, falamos apenas da limiarização baseada em uma única variável: intensidade dos tons de cinza. Em alguns casos, um sensor pode disponibilizar mais de uma variável para identificar cada pixel em uma imagem e, assim, permitir uma limiarização multivariada. Um exemplo notável é a imagem em cores, na qual os componentes são vermelho (R), verde (G) e azul (B). Neste caso, cada “pixel” é identificado por três valores e pode ser representado como um vetor 3-D, \(z = (z_1+z_2+z_3)^T\), cujos componentes são as cores RGB em um ponto. Estes pontos 3-D são frequentemente chamados de voxels para denotar elementos volumétricos em oposição aos elementos de imagem [2, p. 501].

Numa limiarização focada na intensidade de cinza, de apenas uma variável, avaliamos apenas a intensidade, um gráfico de duas variáveis (histograma convencional). A sua limiarização é simples. Já no R, G, B, gráfico tridimensional, avaliamos a distância dos pixels da imagem a um píxel de referência, e o limiar é representado pelo contorno de uma figura geométrica simétrica, como a esfera abaixo, na qual contém os pixels segmentados e tem como seu centro o pixel de referência. Conforme demonstrado na Figura 6.55.

Figura 6.55: Segmentação multivariada no RGB. Gráfico 3-D [2, p. 295].

Suponha que queiramos extrair de uma imagem colorida todas as regiões com uma faixa de cor específica: por exemplo, tons avermelhados da Figura 6.56(a). Vamos denotar a cor avermelhada média em que estamos interessados, a amostra da imagem é demarcada pelo retângulo de bordas claras e finais em Figura 6.56 (a). Uma forma de segmentar uma imagem colorida com base neste parâmetro é calcular uma medida de distância, \(D(z, a)\), entre um ponto de cor arbitrária, \(z\), e a cor média, \(a\) para assim segmentar. A Figura 6.56(b) mostra o resultado desse algoritmo.

\[ g= \begin{cases} 1,\ se\ D(z,a)\ <\ T\\ 0,\ caso\ contrário \end{cases} \tag{6.71}\]

Figura 6.56: Exemplo de segmentação multivariada no RGB [2, p. 295].

Porém, esse cálculo de distância dos pontos ao centro em formato esférico é trabalhoso para o computador. Uma maneira mais eficiente é usar um delimitador cúbico. Nessa metodologia, o cubo é centralizado em \(a\) e suas dimensões ao longo de cada um dos eixos de cor são escolhidas em proporção ao desvio padrão das amostras da imagem ao longo de cada um dos eixos (R, G e B).

Portanto, o procedimento da Figura 6.56(a) consistiu em calcular o vetor médio \(a\) utilizando os pontos de cor contidos no retângulo. Em seguida, calculou-se o desvio padrão dos componentes vermelho, verde e azul dessas amostras. Um cubo foi centralizado em \(a\), e as dimensões ao longo de cada um dos eixos RGB são o valor de \(1.25\) multiplicado pelo \(\sigma\) ao longo dos eixos correspondentes, por exemplo, no eixo \(R\), vermelho, a dimensão do cubo é de \((a_R - 1.25\sigma_R)\) até \((a_R + 1.25\sigma_R)\), no qual \(a_R\) indica o valor do componente vermelho de \(a\). E, por fim, limiarizou-se a Figura.

Refêrencias

[2] R. C. Gonzalez e R. C. Woods, Processamento digital de imagens, 3º ed. São Paulo: Pearson Prentice Hall, 2010.

[3] H. Pedrini e W. Robson Schwartz, Analise de imagens digitais: principios, algoritmos e aplicações, 3º ed. São Paulo: Thomson Learning Edicoes Ltda, 2007.

[9] W. Burger, M. J. Burge, M. J. Burge, e M. J. Burge, Principles of digital image processing, vol. 111. Springer, 2009.

[17] J. Canny, “A computational approach to edge detection”, IEEE Transactions on pattern analysis and machine intelligence, nº 6, p. 679–698, 1986.

[18] M. Sonka, V. Hlavac, e R. Boyle, Image processing, analysis, and machine vision. Cengage Learning, 2014.

[19] M. Nixon e A. Aguado, Feature extraction and image processing for computer vision. Academic press, 2019.

[20] Nasa, “Hubble Ultra-Deep Field”. 2004, [Online]. Disponível em: https://imgsrc.hubblesite.org/hu/db/images/hs-2014-27-a-full_jpg.jpg.

[21] H. Bay, T. Tuytelaars, e L. Van Gool, “Surf: Speeded up robust features”, p. 404–417, 2006.

[22] K. Cen, “Study of Viola-Jones Real Time Face Detector”, 2016.

---

2. Esses limiares podem ser adquiridos a partir de diferentes métodos, como serão explicados nos próximos tópicos.↩︎

3. O uso desses termos não é universal e é provável vê-los sendo utilizados indiferentemente na literatura de processamento de imagens.↩︎

4. A limiarização com dois limiares às vezes é chamada histerese de limiarização.↩︎