Capítulo 5 Filtros Digitais

Filtros digitais representam um conjunto de ferramentas poderosas para realizar operações em imagens. Diferente das operações de ponto que operam sobre um único pixel, as operações utilizando filtros levam em consideração os pixels próximos ao pixel que atualmente está em modificação. Isso nos permite realizar alterações muito mais complexas do que as realizadas anteriormente. Como exemplos disso podemos considerar a operação sharpen (aguçamento) e blur (suavização), que podem ser observados na Figura 5.1(a) e (b), respectivamente.

Figura 5.1: Imagem de ônibus com filtro de aguçamento e de suavização[9, p. 98]

5.1 Convolução

A convolução é uma operação muito utilizada em PDI tendo suas origens na matemática, onde é definida como uma operação realizada entre duas funções que resulta numa terceira. Em outras palavras, a convolução recebe dois sinais como entrada e gera um sinal como saída. No caso de PDI, podemos imaginar os sinais de entrada como sendo a nossa imagem original e o kernel do filtro, e a nossa saída como sendo a imagem filtrada.

Quando dizemos kernel, estamos nos referindo a uma função ou, no caso de PDI, a uma matriz que é aplicada a nossa imagem usando a convolução que irá produzir outra imagem como saída. Na Tabela 5.1, temos exemplos de alguns tipos de kernels que podem ser utilizados na convolução e seus respectivos resultados. Além dos efeitos mais comuns, como o de desfoque (blur), podemos utilizar kernels que extraiam informações mais complexas das imagens, como os detectores de borda, que serão explicados nos próximos tópicos.

Tabela 5.1: Exemplo de kernels (adaptada de [14]).

Operação	Kernel	Resultado
Identidade (Imagem Original)	\[\begin{bmatrix} 0 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0 \end{bmatrix}\]
Detecção de borda	\[\begin{bmatrix} -1 & -1 & -1\\ -1 & 8 & -1\\ -1 & -1 & -1 \end{bmatrix}\]
Média (box blur)	\[\frac{1}{9}\begin{bmatrix} 1 & 1 & 1\\ 1 & 1 & 1\\ 1 & 1 & 1 \end{bmatrix}\]
Gaussian blur	\[\frac{1}{16}\begin{bmatrix} 1 & 2 & 1\\ 2 & 4 & 2\\ 1 & 2 & 1 \end{bmatrix}\]

Em porcessamento de sinais, a operação de convolução, geralmente, é representada pelo símbolo \(*\) e pode ser descrita, em poucas palavras, como uma soma de produtos entre um ponto do kernel e um ponto correspondente da imagem. Essa correspondência é encontrada fazendo um deslizamento sobre a imagem de entrada. A Figura 5.2 representa de maneira visual a convolução em um cenário de uma dimensão, através do sinal de entrada (signal) e o kernel. Pode-se ainda perceber que o kernel está rotacionado em 180º, pelo fato da definição de convolução.

Figura 5.2: Convolução unidimensional[15].

Algo interessante que podemos observar na Figura 5.2 é que nosso sinal de entrada é quase totalmente 0 e contém um único ponto com o valor 1, assim, nosso resultado será uma cópia do kernel. A partir disso, conseguimos imaginar o porquê de termos como resultado a própria imagem quando aplicado um kernel identidade, como mostrado na primeira linha da Tabela 5.1.

Antes de irmos mais adiante no assunto, é importante serem esclarecidos alguns conceitos para que não se tornem confusos. Existe outra operação matemática extremamente parecida com a convolução, que é chamada de correlação, com a diferença de que não se rotaciona o kernel.

Para entendermos bem essa diferença, podemos observar a Figura 5.3, onde temos um exemplo de correlação e convolução sendo executados em um espaço unidimensional. Temos uma função \(f\) e um filtro \(w\) na Figura 5.3(a) e (b), respectivamente. Na sequência, em (b) e (j), temos as funções e os filtros prontos para iniciar a correlação e a convolução. Nas etapas (c) e (k), podemos ver o preenchimento com zeros, porque há partes das funções que não se sobrepõem, dessa forma, permite que \(w\) percorra todos os pixels de \(f\). Após isso, é realizado o primeiro passo da correlação e convolução, onde podemos observar que o resultado é 0, já que \(w\) está sobreposto por somente zeros; logo, a soma da multiplicação de cada item de \(w\) por \(f\) será zero. Desloca-se, então, o filtro \(w\) em uma unidade à direita, onde o resultado novamente será 0. O primeiro resultado não nulo se dará no terceiro deslocamento, sendo 8 para a correlação e \(1\) para a convolução. Temos o resultado de ambas operações em (g) e (o), e o resultado recortado em (h) e (p) que remove os zeros até o tamanho ficar igual ao da \(f\) inicial.

Figura 5.3: Ilustração de correlação e convolução unidimensional[2, p. 96].

Vamos extender agora essas duas operações à aplicação em duas dimensões. Uma representação disso pode ser vista na Figura 5.4, onde temos novamente o kernel \(w\) e a função \(f\). Percebe-se, novamente, o efeito de se aplicar o kernel em uma imagem com apenas o número 1 no meio, nos dois casos temos como saída a cópia do kernel aplicado, com a diferença que na correlação o kernel aparece rotacionado no resultado. Assim, nota-se que, se pré-rotacionarmos, a correlação produzirá o mesmo que uma convolução.

Já que a correlação e convolução são iguais, é preciso saber qual delas utilizar. Segundo Gonzalez, [2, p. 98], isso é uma questão de preferência e qualquer uma das duas operações conseguem realizar a outra com uma simples rotação do kernel. Essa questão se torna ainda menos relevante quando utilizamos filtros que são simétricos, pois temos o mesmo kernel antes e após a rotação, logo, tanto na correlação quanto na convolução, nos darão o mesmo resultado. Entretanto, usando kernels assimétricos, temos resultados diferentes. Conforme Moeslund, [4, p. 87], quando trabalhamos com filtros de desfoque, detectores de borda, entre outros, o processo de se aplicar o kernel é comumente chamado de convolução mesmo quando na prática se é feita a correlação.

Figura 5.4: Ilustração de correlação e convolução bidimensional[2, p. 98].

5.1.1 Definção matemática da convolução

Vamos explorar um pouco das notações matemáticas utilizadas para representar a convolução e a correlação, pois, assim, também poderemos consolidar a idéia de como são tão similares. Como dito no início desta seção, geralmente, a convolução é identificada por \(*\) e a correlação por \(\star\). A correlação em duas dimensões segue a Equação (5.1)

\[g(x,y) = w(x,y)\star f(x,y) = \sum_{s=-a}^{a}\sum_{t=-b}^{b}\ w(s,t)f(x+s,y+t) \tag{5.1}\]

em que \(w\) é nosso \(kernel\) e \(f\) nossa imagem. Percebe-se que ambas são funções de duas variáveis, \(x\) e \(y\), pois estamos trabalhando em duas dimensões. Os limites dos somatórios são dados por \(a=(m-1)/2\) e \(b=(n-1)/2\) e o que essa função faz é andar em cada posição da imagem, ou seja, \((x,y)\), e substituir o pixel atual pela soma de produtos entre os valores do \(kernel\) e os valores dos pixels da imagem. Já a convolução tem uma equação bem similar, sendo diferente apenas pelos sinais negativos em \(f\), o que evidência a rotação do \(kernel\). Pode-se notar que os sinais inversos estão em \(f\) e não em \(w\). Segundo Gonzalez[2, p. 98], isso é usado para fins de simplicidade de notação e não alteram o resultado.

\[g(x,y) = w(x,y)*f(x,y) = \sum_{s=-a}^{a}\sum_{t=-b}^{b}\ w(s,t)f(x-s,y-t)\].

Uma das melhores maneiras de entender bem as equações é através de um exemplo prático. A seguir, um exemplo passo-a-passo de correlação:

Etapa 1 de 9

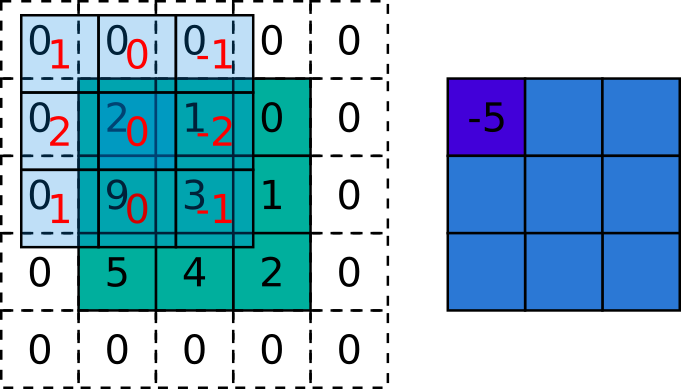
\[ \begin{gathered} \text{w}\text{*f}\left(0,0\right)\text{=}\sum_{s}^{}\sum_{t}^{}\text{w}\left(s,t\right)\text{f}\left(0+s,0+t\right)\,\text{=}\,\\ \text{+w}\left(-1,-1\right)\text{f}\left(-1,-1\right)\text{+w}\left(-1,0\right)\text{f}\left(-1,0\right)\text{+w}\left(-1,1\right)\text{f}\left(-1,1\right)\\ \text{+w}\left(0,-1\right)\text{f}\left(0,-1\right)\text{+w}\left(0,0\right)\text{f}\left(0,0\right)\text{+w}\left(0,1\right)\text{f}\left(0,1\right)\\ \text{+w}\left(1,-1\right)\text{f}\left(1,-1\right)\text{+w}\left(0,1\right)\text{f}\left(0,-1\right)\text{+w}\left(1,1\right)\text{f}\left(-1,-1\right)\\ =\,1\cdot0+0\cdot0+\left(-1\right)\cdot0\\ +2\cdot0+0\cdot2+\left(-2\right)\cdot1\\ +1\cdot0+0\cdot9+\left(-1\right)\cdot3\\ =0\,-2-3\,=\,-5 \end{gathered} \]

Etapa 2 de 9

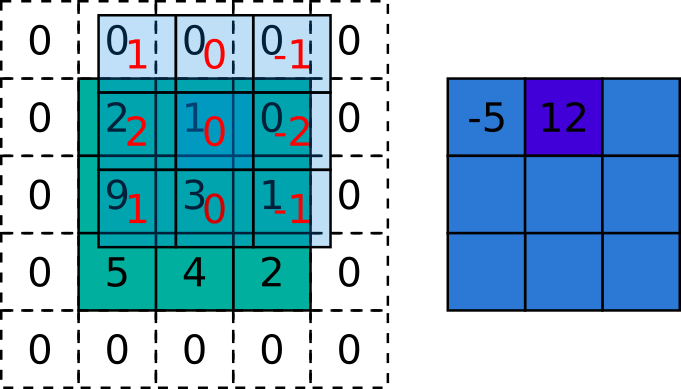
\[ \begin{gathered} \text{w}\text{*f}\left(0,1\right)\text{=}\sum_{s}^{}\sum_{t}^{}\text{w}\left(s,t\right)\text{f}\left(0+s,1+t\right)\,\text{=}\, \\ \text{+w}\left(-1,-1\right)\text{f}\left(-1,0\right)\text{+w}\left(-1,0\right)\text{f}\left(-1,1\right)\text{+w}\left(-1,1\right)\text{f}\left(-1,2\right)\\ \text{+w}\left(0,-1\right)\text{f}\left(0,0\right)\text{+w}\left(0,0\right)\text{f}\left(0,1\right)\text{+w}\left(0,1\right)\text{f}\left(0,2\right)\\ \text{+w}\left(1,-1\right)\text{f}\left(1,0\right)\text{+w}\left(1,0\right)\text{f}\left(1,1\right)\text{+w}\left(1,1\right)\text{f}\left(1,2\right)\\ =\,1\cdot0+0\cdot0+\left(-1\right)\cdot0\\ +2\cdot2+0\cdot1+\left(-2\right)\cdot0\\ +1\cdot9+0\cdot3+\left(-1\right)\cdot1\\ =0\,+4+8=\,12 \end{gathered} \]

Etapa 3 de 9

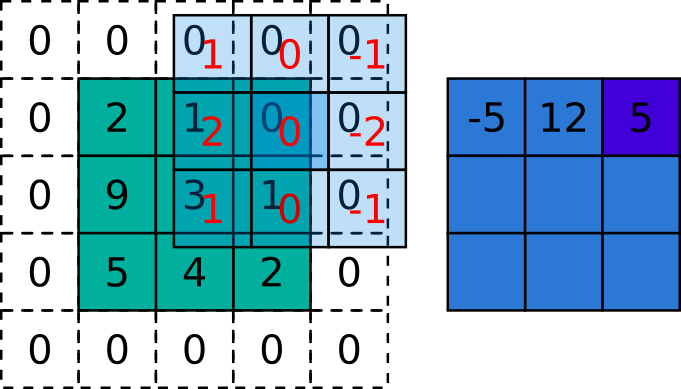\[ \begin{gathered} \text{w}\text{*f}\left(0,2\right)\text{=}\sum_{s}^{}\sum_{t}^{}\text{w}\left(s,t\right)\text{f}\left(0+s,2+t\right)\,\text{=}\,\\ \text{+w}\left(-1,-1\right)\text{f}\left(-1,1\right)\text{+w}\left(-1,0\right)\text{f}\left(-1,2\right)\text{+w}\left(-1,1\right)\text{f}\left(-1,3\right)\\ \text{+w}\left(0,-1\right)\text{f}\left(0,1\right)\text{+w}\left(0,0\right)\text{f}\left(0,2\right)\text{+w}\left(0,1\right)\text{f}\left(0,3\right)\\ \text{+w}\left(1,-1\right)\text{f}\left(1,1\right)\text{+w}\left(1,0\right)\text{f}\left(1,2\right)\text{+w}\left(1,1\right)\text{f}\left(1,3\right)\\ =\,1\cdot0+0\cdot0+\left(-1\right)\cdot0\\ +2\cdot1+0\cdot0+\left(-2\right)\cdot0\\ +1\cdot3+0\cdot1+\left(-1\right)\cdot0\\ =0\,+2+3=\,5 \end{gathered} \]

Etapa 4 de 9

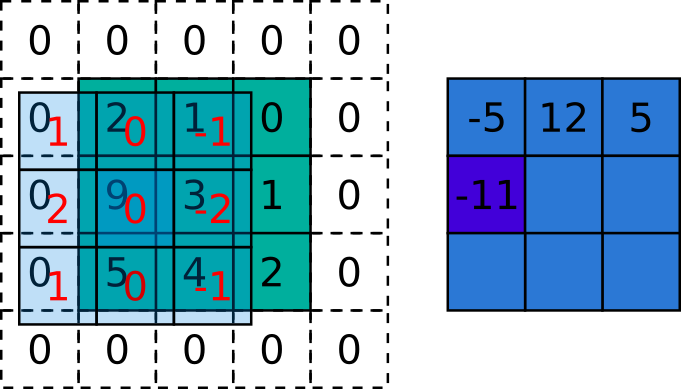\[ \begin{gathered} \text{w}\text{*f}\left(1,0\right)\text{=}\sum_{s}^{}\sum_{t}^{}\text{w}\left(s,t\right)\text{f}\left(1+s,0+t\right)\,\text{=}\,\\ \text{+w}\left(-1,-1\right)\text{f}\left(0,-1\right)\text{+w}\left(-1,0\right)\text{f}\left(0,0\right)\text{+w}\left(-1,1\right)\text{f}\left(0,1\right)\\ \text{+w}\left(0,-1\right)\text{f}\left(1,-1\right)\text{+w}\left(0,0\right)\text{f}\left(1,0\right)\text{+w}\left(0,1\right)\text{f}\left(1,1\right)\\ \text{+w}\left(1,-1\right)\text{f}\left(2,-1\right)\text{+w}\left(1,0\right)\text{f}\left(2,0\right)\text{+w}\left(1,1\right)\text{f}\left(2,1\right)\\ =\,1\cdot0+0\cdot2+\left(-1\right)\cdot1\\ +2\cdot0+0\cdot9+\left(-2\right)\cdot3\\ +1\cdot0+0\cdot5+\left(-1\right)\cdot4\\ =\left(-1\right)\,+\left(-6\right)+\left(-4\right)=\,-11 \end{gathered} \]

Etapa 5 de 9

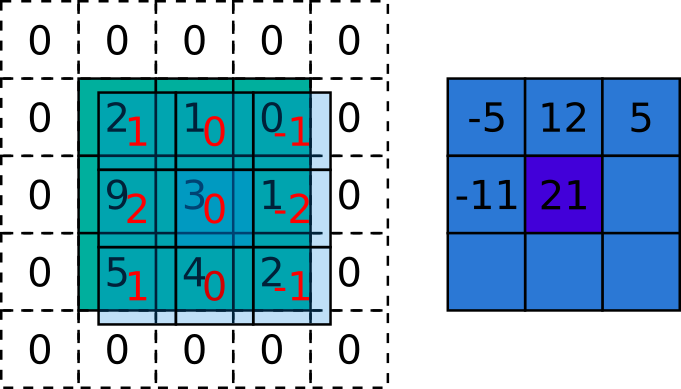\[ \begin{gathered} \text{w}\text{*f}\left(1,1\right)\text{=}\sum_{s}^{}\sum_{t}^{}\text{w}\left(s,t\right)\text{f}\left(1+s,1+t\right)\,\text{=}\,\\ \text{+w}\left(-1,-1\right)\text{f}\left(0,0\right)\text{+w}\left(-1,0\right)\text{f}\left(0,1\right)\text{+w}\left(-1,1\right)\text{f}\left(0,2\right)\\ \text{+w}\left(0,-1\right)\text{f}\left(1,0\right)\text{+w}\left(0,0\right)\text{f}\left(1,1\right)\text{+w}\left(0,1\right)\text{f}\left(1,2\right)\\ \text{+w}\left(1,-1\right)\text{f}\left(2,0\right)\text{+w}\left(1,0\right)\text{f}\left(2,1\right)\text{+w}\left(1,1\right)\text{f}\left(2,2\right)\\ =\,1\cdot2+0\cdot1+\left(-1\right)\cdot0\\ +2\cdot9+0\cdot3+\left(-2\right)\cdot1\\ +1\cdot5+0\cdot4+\left(-1\right)\cdot2\\ =2\,+16+3=\,21 \end{gathered} \]

Etapa 6 de 9

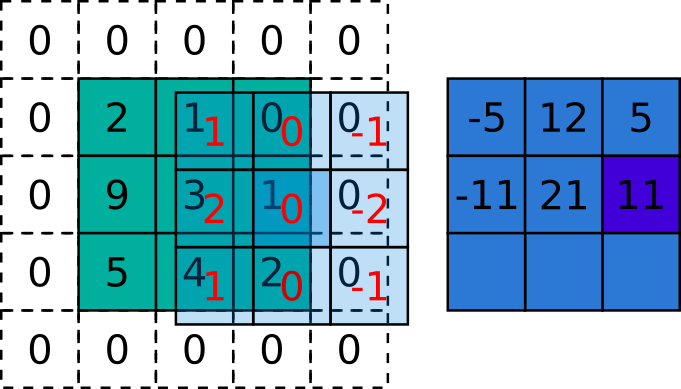\[ \begin{gathered} \text{w}\text{*f}\left(1,2\right)\text{=}\sum_{s}^{}\sum_{t}^{}\text{w}\left(s,t\right)\text{f}\left(1+s,2+t\right)\,\text{=}\,\\ \text{+w}\left(-1,-1\right)\text{f}\left(0,1\right)\text{+w}\left(-1,0\right)\text{f}\left(0,2\right)\text{+w}\left(-1,1\right)\text{f}\left(0,3\right)\\ \text{+w}\left(0,-1\right)\text{f}\left(1,1\right)\text{+w}\left(0,0\right)\text{f}\left(1,2\right)\text{+w}\left(0,1\right)\text{f}\left(1,3\right)\\ \text{+w}\left(1,-1\right)\text{f}\left(2,1\right)\text{+w}\left(1,0\right)\text{f}\left(2,2\right)\text{+w}\left(1,1\right)\text{f}\left(2,3\right)\\ =\,1\cdot1+0\cdot1+\left(-1\right)\cdot0\\ +2\cdot3+0\cdot1+\left(-2\right)\cdot0\\ +1\cdot4+0\cdot2+\left(-1\right)\cdot0\\ =1\,+6+4=\,11 \end{gathered} \]

Etapa 7 de 9

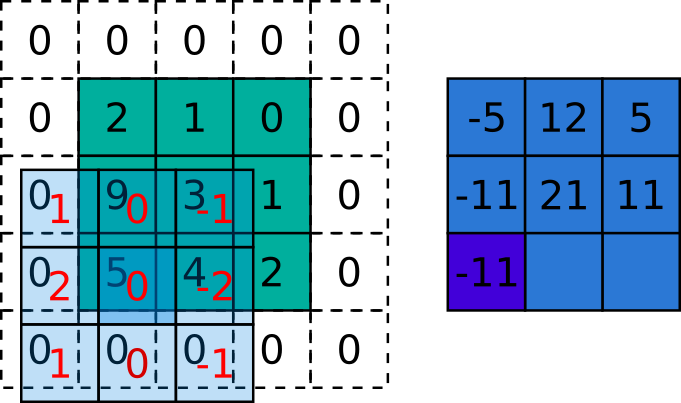\[ \begin{gathered} \text{w}\text{*f}\left(2,0\right)\text{=}\sum_{s}^{}\sum_{t}^{}\text{w}\left(s,t\right)\text{f}\left(2+s,0+t\right)\text{=}\\ \text{+w}\left(-1,-1\right)\text{f}\left(1,-1\right)\text{+w}\left(-1,0\right)\text{f}\left(1,0\right)\text{+w}\left(-1,1\right)\text{f}\left(1,1\right)\\ \text{+w}\left(0,-1\right)\text{f}\left(2,-1\right)\text{+w}\left(0,0\right)\text{f}\left(2,0\right)\text{+w}\left(0,1\right)\text{f}\left(2,1\right)\\ \text{+w}\left(1,-1\right)\text{f}\left(3,-1\right)\text{+w}\left(1,0\right)\text{f}\left(3,0\right)\text{+w}\left(1,1\right)\text{f}\left(3,1\right)\\ =\,1\cdot0+0\cdot9+\left(-1\right)\cdot3\\ +2\cdot0+0\cdot5+\left(-2\right)\cdot4\\ +1\cdot0+0\cdot0+\left(-1\right)\cdot0\\ =\left(-3\right)+\left(-8\right)+0=\,-11 \end{gathered} \]

Etapa 8 de 9

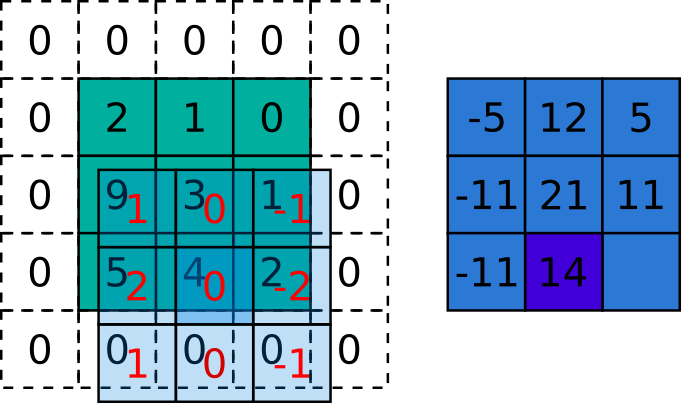\[ \begin{gathered} \text{w}\text{*f}\left(2,1\right)\text{=}\sum_{s}^{}\sum_{t}^{}\text{w}\left(s,t\right)\text{f}\left(2+s,1+t\right)\,\text{=}\,\\ \text{+w}\left(-1,-1\right)\text{f}\left(1,0\right)\text{+w}\left(-1,0\right)\text{f}\left(1,1\right)\text{+w}\left(-1,1\right)\text{f}\left(1,2\right)\\ \text{+w}\left(0,-1\right)\text{f}\left(2,0\right)\text{+w}\left(0,0\right)\text{f}\left(2,1\right)\text{+w}\left(0,1\right)\text{f}\left(2,2\right)\\ \text{+w}\left(1,-1\right)\text{f}\left(3,0\right)\text{+w}\left(1,0\right)\text{f}\left(3,1\right)\text{+w}\left(1,1\right)\text{f}\left(3,2\right)\\ =\,1\cdot9+0\cdot3+\left(-1\right)\cdot1\\ +2\cdot5+0\cdot4+\left(-2\right)\cdot2\\ +1\cdot0+0\cdot0+\left(-1\right)\cdot0\\ =8+6+0=\,14 \end{gathered} \]

Etapa 9 de 9

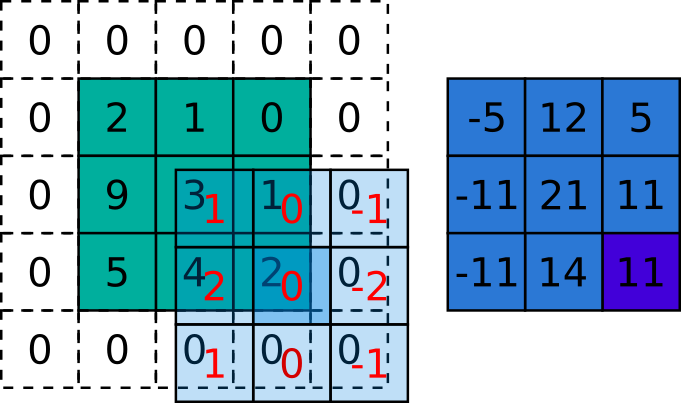\[ \begin{gathered} \text{w}\text{f}\left(2,2\right)\text{=}\sum{s}^{}\sum{t}^{}\text{w}\left(s,t\right)\text{f}\left(2+s,2+t\right)\text{=}\\ \text{+w}\left(-1,-1\right)\text{f}\left(1,1\right)\text{+w}\left(-1,0\right)\text{f}\left(1,2\right)\text{+w}\left(-1,1\right)\text{f}\left(1,3\right)\\ \text{+w}\left(0,-1\right)\text{f}\left(2,1\right)\text{+w}\left(0,0\right)\text{f}\left(2,2\right)\text{+w}\left(0,1\right)\text{f}\left(2,3\right)\\ \text{+w}\left(1,-1\right)\text{f}\left(3,1\right)\text{+w}\left(1,0\right)\text{f}\left(3,2\right)\text{+w}\left(1,1\right)\text{f}\left(3,3\right)\\ =,1\cdot3+0\cdot1+\left(-1\right)\cdot0\\ +2\cdot4+0\cdot2+\left(-2\right)\cdot0\\ +1\cdot0+0\cdot0+\left(-1\right)\cdot0\\ =3+8+0=11 \end{gathered} \]

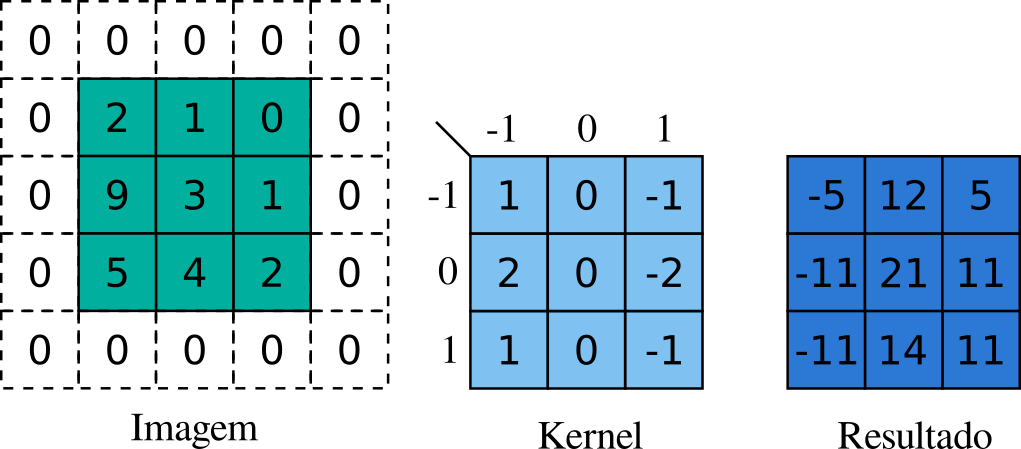
Figura 5.5: Exemplo da aplicação da correlação sobre uma imagem. A matriz verde é a imagem, a azul claro é o kernel e a azul escuro é a imagem resultante. Fonte: autoria própria inspirado em http://www.songho.ca/dsp/convolution/convolution2d_example.html e https://arxiv.org/abs/1603.07285.

O exemplo utiliza um \(kernel\) assimétrico. Então, os resultados da correlação e convolução são diferentes. Deixaremos isso como um exercício ao leitor, realizar a convolução para provar essa diferença. O caso anterior também tem uma característica que é o complemento das bordas com 0’s, constant padding, para que o \(kernel\) pudesse ser aplicado sobre toda a imagem. A seguir, tem-se métodos alternativos para lidar com essa característica[9, p. 125], [16, p. 60]:

• Preenchimento com constante (constant padding): Método onde as laterais são preenchidas com um valor constante, comumente 0.

• Preenchimento com vizinho (nearest neighbor): Se realiza o preenchimento das bordas adicionais com os valores dos vizinhos mais próximos.

• Reflexão (reflect): Os pixels das bordas da imagem são repetidos nas bordas adicionais.

• Repetição (ou wrap): A imagem é repetida nas bordas.

Além dos métodos apresentados, existem outras técnicas que podem ser utilizadas, sendo que em cada caso se escolhe a que melhor se ajusta à tarefa realizada.

O último ponto a ser explorado é a escolha do tamanho ideal do preenchimento que deve ser aplicado à imagem. De forma geral, se temos uma imagem (\(f\)), um kernel (\(w\)) e um preenchimento (\(p\)), podemos escrever a seguinte relação¹(5.2)

\[saída = (f_{vertical} - w_{vertical} + p_{vertical} + 1) \times (f_{horizontal} - w_{horizontal} + p_{horizontal} + 1) \tag{5.2}\]

Isso nos leva a perceber que o tamanho da imagem de saída aumenta conforme o preenchimento. Na maioria dos casos, queremos que a imagem de entrada e saída tenha o mesmo tamanho, então, usamos \(p_{vertical} = k_{vertical} - 1\) e \(p_{horizontal} = k_{horizontal} - 1\). E, como o kernel tem tamanho ímpar geralmente, utilizamos \(\frac{p_{vertical}}{2}\) e \(\frac{p_{horizontal}}{2}\).

5.2 Filtro da Média

O filtro da média é um tipo de filtro que utiliza a média dos valores dos pixels próximos ao pixel central. Como esse tipo de filtro realiza uma operação linear, ele é classificado como um filtro linear de suavização [2, p. 101]. Essa suavização se dá exatamente pelo tipo da operação utilizada, a média dos pixels vizinhos, que diminui a nitidez pela redução das transições abruptas nos níveis de intensidade. Um dos problemas que podem ocorrer é que as bordas também são mudanças abruptas, então podem ser comprometidas pelo filtro[2, p. 101]. Na Figura 5.6, temos um exemplo do efeito desse filtro.

Figura 5.6: Imagem de ônibus com filtro de aguçamento e de suavização[9, p. 98].

A máscara (kernel) de um filtro de média 3x3 pode ser representada por (5.3):

\[\begin{bmatrix} \frac{1}{9} & \frac{1}{9} & \frac{1}{9}\\ \frac{1}{9} & \frac{1}{9} & \frac{1}{9}\\ \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \end{bmatrix} = \frac{1}{9} \begin{bmatrix} 1 & 1 & 1\\ 1 & 1 & 1\\ 1 & 1 & 1 \end{bmatrix} \tag{5.3}\] A primeira forma é a soma de todos os valores divididos por 9, o qual é o tamanho do filtro. A segunda forma, onde todos os coeficientes do kernel são 1’s, é mais eficiente computacionalmente, pois realizamos todas as somas e multiplicações antes de dividirmos. Esse tipo de filtro é muitas vezes chamado de box filter.

Figura 5.7: Imagem com diferentes tamanhos de filtro de média. (b) a (f) resultados da suavização com filtros quadrados de tamanhos 3, 5, 9, 15 e 35, respectivamente.[2, p. 102].

Na Figura 5.7, temos um exemplo onde foram aplicados filtros de média com diferentes tamanhos, 3x3(b), 5x5(c), 9x9(d), 15x15(e) e 35x35(f). Podemos notar que com o menor filtro, o de tamanho 3, temos um leve borramento na imagem toda, mas que as partes que tem o mesmo tamanho ou são menores que o filtro tem um borramento maior. Isso exemplifica umas das importantes aplicações dos filtros de suavização, que é a de desfocar os objetos menores e deixar os maiores em maior evidência[2, p. 101].

Figura 5.8: Exemplo de uso do desfoque através de um kernel 15x15 para uma melhor segmentação[2, p. 103].

Na Figura 5.8, podemos ver como o desfoque pode ser utilizado para encontrar os detalhes principais da imagem. Nesta imagem obtida a partir do telescópio Hubble, foi aplicado o desfoque para diminuir a visibilidade dos objetos menores e dar maior ênfase aos da frente. E, então, foi limiarizado o resultado a fim de destacar esses objetos. A limiarização é um método de segmentação, que será explicado em sua devida seção.

5.3 Filtro da Mediana

A mediana é um filtro não linear que utiliza como princípio a própria técnica estatística, que consiste em colocar um conjunto de dados em ordem e selecionar o valor central. Esse tipo de filtro é muito eficiente na remoção de ruído, principalmente, o tipo de ruído conhecido como ruído sal e pimenta, que são os ruídos impulsivos[2, p. 102]. Como dito anteriormente, a mediana consiste em ordenar o conjunto de dados e ter como saída o valor do 50º percentil, nesse caso o conjunto de dados são os valores dos pixels da imagem. Assim, para um kernel de tamanho 3x3, o valor desse pixel na imagem de saída será o quinto maior valor de intensidade.

Na Figura 5.9, temos um exemplo mostrando uma imagem de raios-X de uma placa de circuitos eletrônicos com a presença de ruído tipo sal e pimenta, 5.9(a). A figura também apresenta as respectivas aplicações de um filtro da média, 5.9(b), e do filtro da mediana, 5.9(c), ambos com kernel de tamanho 3x3. É possível perceber o quanto o filtro da mediana se sai melhor na remoção desse tipo de ruído.

Portanto, pela característica da mediana, em ter como saída 50º percentil, pode-se afirmar que agrupamentos de ruídos menores que metade da área do filtro serão removidos[2, p. 102].

Figura 5.9: Remoção de ruído sal e pimenta por meio do filtro de Mediana[2, p. 103].

5.4 Filtro Gaussiano

O Filtro gaussiano é um filtro simétrico (isotrópico) usado para suavizar imagens. Ele é um filtro de média ponderada, mas com seus pesos seguindo aproximadamente uma distribuição gaussiana. O “aproximadamente” é pelo fato que será necessário truncamentos, havendo erros, e caso opte pela função modificada, (5.5), ao invés da original, (5.4). Ao usar a função modificada, sem a constante multiplicadora, o perfil da função fica melhor, variando os pesos do kernel de (0, 1], conforme Figura 5.10.

• Função gaussiana: \[G(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \tag{5.4}\]

• Função gaussiana modificada: \[G'(x) = e^{-\frac{(x-\mu)^2}{2\sigma^2}} \tag{5.5}\]

Note que, na Figura 5.10, a função tem formato de sino, variando de acordo com os valores atribuídos ao \(\sigma\), que dependerá da ênfase desejada no cálculo. A medida que \(\sigma\) aumenta, maior é o peso dado às “caldas” da função, isto é, aos pixels mais distantes do centro do kernel. Essa característica é representada no gráfico da Figura 5.10.

A fim de que o pixel central da máscara esteja em \((0,0)\), considera-se \(\mu=0\).

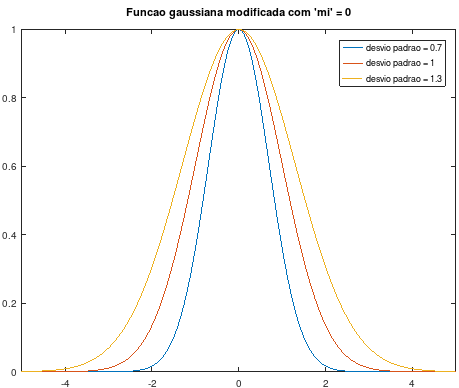
Figura 5.10: Função gaussiana com \(\mu=0\) e diferentes \(\sigma\)

O Filtro Gaussiano 2D pode ser gerado através da convolução de dois vetores resultantes de \(G'(x)\) sendo \(x\) ora as linhas, representando um vetor da matriz 2D, ora as colunas, representando o outro vetor da matriz 2D. De forma alternativa, ele também pode ser construído a partir da n-ésima linha do Triângulo de Pascal que corresponde ao tamanho do kernel desejado [3, p. 126]. Como o método é o mesmo para as duas fontes, optamos explicá-lo pela função gaussiana modificada, (5.5).

O procedimento primário é obter a imagem da função, mas, para obter um filtro com intuito gaussiano, deve-se selecionar a amostragem dos pontos no intervalo de \(\pm 2.5\sigma\) ou \(\pm 3.5\sigma\) [9, p. 114]. Assim, escolhendo a primeira opção, para modelagem de um kernel 7x7, procura-se \(G'(0)\), \(G'(1)\), \(G'(2)\) e \(G'(3)\), pela simetria da função, esses valores já bastam, conforme demonstrado em (5.6). Entretanto, como os valores têm infinitas casas decimais, devem ser truncados. Aqui escolhemos o uso de cinco casas decimais.

\[\begin{split} &G'(-3) = G'(3) = 0,01110\\ &G'(-2) = G'(2) = 0,13533\\ &G'(-1) = G'(1) = 0,60653\\ &G'(0) = 1 \end{split} \tag{5.6}\]

Então, considera-se o menor valor como 1, no caso \(G'(3)\) e \(G'(-3)\), e interpolamos os demais, truncando-os com propósito de obter a parte inteira. A divisão por 224 é oriunda da soma dos coeficientes encontrados no vetor. Pronto, temos a máscara gaussiana 1D (5.7).

\[\frac{1}{224}\begin{bmatrix}1 & 12 & 54 & 90 & 54 & 12 & 1\end{bmatrix} \tag{5.7}\]

Com a máscara em mãos, convoluciona-se os seguintes fatores:

• \(\frac{1}{224}\begin{bmatrix}1 & 12 & 54 & 90 & 54 & 12 & 1\end{bmatrix}\)

• \(\frac{1}{224}\begin{bmatrix}1 \\ 12 \\ 54 \\ 90 \\ 54 \\ 12 \\ 1\end{bmatrix}\)

• \(f(x,y)\) é a imagem de entrada

Há uma determinada ordem do cálculo que é mais eficiente para o sistema digital, que é a convolução entre \(f(x,y)\) e uma das máscaras 1D e a convolução desse resultado com a transposta desse kernel. Pronto, tem-se o filtro gaussiano 2D aplicado a imagem como saída.

Figura 5.11: Imagem com diferentes tamanhos de filtro gaussiano. Adaptado de [2, p. 102]

Na Figura 5.11, tem-se um exemplo similar ao usado no filtro de média, porém, usando-se o filtro gaussiano. A imagem de entrada (a) tem tamanho 500x500 onde foram aplicados filtros de diferentes tamanhos, 3x3(b), 5x5(c), 9x9(d), 15x15(e) e 35x35(f). Note que, ao contrário do exemplo anterior, Figura 5.7, há uma maior preservação da nitidez, todavia não seria um filtro eficiente para redução de ruído. Essa característica é devido ao maior peso dado aos pixels quão mais próximo do centro do kernel estão.

Refêrencias

[2] R. C. Gonzalez e R. C. Woods, Processamento digital de imagens, 3º ed. São Paulo: Pearson Prentice Hall, 2010.

[3] H. Pedrini e W. Robson Schwartz, Analise de imagens digitais: principios, algoritmos e aplicações, 3º ed. São Paulo: Thomson Learning Edicoes Ltda, 2007.

[4] T. B. Moeslund, Introduction to video and image processing: Building real systems and applications. Springer Science & Business Media, 2012.

[9] W. Burger, M. J. Burge, M. J. Burge, e M. J. Burge, Principles of digital image processing, vol. 111. Springer, 2009.

[14] W. Commons, “Kernel (image processing)”. 2011, [Online]. Disponível em: https://en.wikipedia.org/wiki/Kernel_(image_processing).

[15] T. e2eML Course Catalog, “Convolution in one dimension for neural networks”. 2020, [Online]. Disponível em: https://e2eml.school/convolution_one_d.html.

[16] R. CHITYALA e S. PUDIPEDDI, Image processing and acquisition using Python. CRC Press, 2020.

---

1. Adaptado de https://d2l.ai/chapter_convolutional-neural-networks/padding-and-strides.html↩︎