Capítulo 7 Deep Learning em visão computacional

Antes de iniciarmos o estudo sobre Deep Learning, e mais especificamente sobre redes neurais artificiais convolucionais, é importante termos uma visão ampla sobre a área e suas subdivisões para conseguirmos nos localizar em meio a essa área que cresce cada vez mais. Por isso começaremos falando um pouco sobre inteligência artificial e suas subdivisões, além de sua conexão e uso com visão computacional, que é o nosso foco.

7.1 Caracterização de IA, Machine Learning e Deep Learning

Esses três termos costumam causar certa confusão, principalmente em pessoas que estão começando a estudar essa área. De maneira geral, o termo Inteligência Artificial (IA) denomina uma área que possui muitas vertentes e tópicos de estudos, onde a maioria tem o foco em conseguir fazer os computadores realizarem tarefas complexas, que anteriormente eram realizadas exclusivamente por humanos.

No começo dos estudos sobre IA foram tentados e resolvidos muitos problemas que eram considerados difíceis para seres humanos, mas relativamente fáceis para os computadores [23, p. 1]. Esses eram problemas que podiam ser descritos formalmente, por meio de regras matemáticas, como exemplo, temos o jogo de xadrez, onde, em 1997, o campeão Garry Kasparov perdeu para o IBM Deep Blue (Figura 7.1).

Figura 7.1: IBM Deep Blue [24].

Com o tempo começamos a perceber que a dificuldade não residia nesses problemas, mas naqueles que são realizados facilmente, até instintivamente e intuitivamente pelos humanos, como reconhecer rostos familiares, entender linguagens, etc. A questão é que os seres humanos, no dia a dia, recebem e processam quantidades enormes de informações, então tentar fazer os computadores realizarem essas atividades somente com regras descritas por nós não era algo viável, por isso os pesquisadores começaram a desenvolver técnicas onde o próprio computador, através de algoritmos, aprendesse a abstrair essas regras e informações sozinho de bases de dados brutos, a isso chamamos de Machine Learning (Aprendizado de Máquina).

Dentro da área de Machine Learning, temos um conjunto de técnicas e áreas de pesquisa, sendo que uma delas utiliza um modelo baseado em cérebros biológicos, contendo neurônios e conexões conhecidas como Redes Neurais. Na Figura 7.2, temos uma representação dos neurônios do córtex cerebral humano, onde podemos ver as conexões formadas por eles, que se assemelham com o modelo de redes neurais da Figura 7.3.

Figura 7.2: Representação da conexão de neurônios no córtex cerebral [25, p. 363].

Atualmente, como ouvimos muito se falar sobre IA’s, temos a tendência de pensar que essa é uma técnica moderna, mas a ideia de fazer os computadores imitarem o esquema de funcionamento do cérebro remonta a 1943, quando Warren McCulloch e Walter Pitts sugeriram a ideia em seu artigo “A logical calculus of the ideas immanent in nervous activity” [26].

Como pode ser visto na Figura 7.3, as redes neurais são formadas por camadas, sendo que os dados entram pela camada Input, são processados nas camadas Hidden e temos os dados de saída na camada Output. Cada uma dessas camadas é formada por um número de neurônios (representados pelos círculos) e suas conexões são representadas pelas setas. Por enquanto, não será aprofundado tanto no funcionamento das redes neurais, isso será abordado na Seção Redes Neurais Artificiais.

Figura 7.3: Rede neural artificial [27].

Nos últimos anos, temos visto um leque de aplicações cada vez maior para as técnicas de IA. Nosso objetivo nesse material é introduzir, principalmente, o uso das redes neurais artificiais na área da visão computacional, que é identificada como uma das subáreas da Inteligência Artificial pois busca reproduzir algumas das capacidades humanas a partir de sistemas autônomos. O principal interesse da visão computacional é fazer com que computadores desempenhem funções semelhantes à visão humana, sendo capazes de receber dados visuais e com eles realizar reconhecimentos, classificações e análises. Análogo ao processo de aprendizado dos seres humanos, identifica-se que a melhora no desempenho da visão computacional está fortemente interligada com a evolução do aprendizado de máquina (machine learning), outro segmento da inteligência artificial.

Antes de entrarmos realmente no assunto de redes neurais, vamos apresentar, resumidamente, alguns tópicos principais da área de machine learning, pois, como dito anteriormente, o deep learning e as redes neurais estão dentro dessa área, e o entendimento desses tópicos podem auxiliar no pleno entendimento dos tópicos futuros.

7.1.1 Aprendizado supervisionado e não supervisionado

Dentro dos algoritmos de machine learning, existe uma característica que os separa em diferentes tipos, baseado em sua forma de aprendizado: os algoritmos de aprendizado supervisionado e não supervisionado.

Na aprendizagem supervisionada, os algoritmos têm previamente os pares de entrada-saída, ou seja, para cada entrada temos o conhecimento prévio de sua a saída [28, p. 695], e, a partir disso, nosso algoritmo deve aprender a generalizar bem as entradas. Podemos formalizar isso da seguinte forma [28, p. 695]:

Dado um conjunto de treinamento de \(n\) pares \((x_1,y_1), (x_2,y_2),\dots,(x_n,y_n)\) onde \(x_i\) são as entradas e \(y_i = f(x_i)\), as saídas, nosso algoritmo deve descobrir a função \(h\), conhecida como hipótese, que melhor aproxime \(f\). Para sabermos se nossa hipótese aproxima bem \(f\), após ter treinado o algoritmo, utilizamos um conjunto de testes - que contém exemplos diferentes do conjunto de treinamento - e avaliamos o quão bem o algoritmo generaliza (dá respostas corretas) as novas entradas.

Já na aprendizagem não supervisionada, não há nenhuma resposta para as saídas do algoritmo, ou seja, ele recebe somente os dados de entrada. Por isso, uma das principais tarefas designadas a esses tipos de algoritmos é a de clustering (agrupamento), onde o algoritmo aprende a encontrar padrões nos dados de entrada e os separam em grupos.

7.1.2 Redes Neurais Artificiais

Parte da base teórica que fundamenta o aprendizado profundo surgiu inicialmente como modelos para entender o aprendizado, ou seja, como o cérebro funciona. Desta forma, estas teorias ficaram conhecidas como Redes Neurais, uma das áreas do aprendizado profundo que mais cresceram nos últimos anos [23, p. 1]. Atualmente, os conceitos de Redes Neurais abordam princípios mais genéricos, não restritos à perspectiva da neurociência. Mesmo que as Redes Neurais não sejam capazes de explicar muito sobre o cérebro, não podendo ser sugeridas como modelos realistas da função biológica, vários aspectos do aprendizado ainda continuam sendo inspirações.

As redes foram pensadas para adquirir o conhecimento por um processo de aprendizagem. Semelhante ao que ocorre no cérebro, as interações entre os neurônios, ou pesos sinápticos, são responsáveis por armazenar o conhecimento. Em termos práticos, o conhecimento de uma rede seria a capacidade de uma máquina em realizar funções complexas de forma autônoma, como classificações e reconhecimentos de padrões. As redes também são capazes de generalizar a informação aprendida, extraindo características essenciais de exemplos e garantindo respostas coerentes aos novos casos [29, p. 28].

Mesmo que o termo Rede Neural só tenha começado a ganhar destaque nos últimos anos, os primeiros estudos teóricos começaram por volta de 1940 [23, p. 12]. Um dos primeiros trabalhos publicados foi “A Logical Calculus of the Ideas Immamente in Nervous Activity” de 1943, em que os autores, Warren McCulloch e Walter Pitts, apresentaram um modelo artificial de um neurônio a partir da teoria de redes lógicas de nós [23, p. 14].

A Figura 7.4 apresenta uma simplificação de um neurônio biológico, dividido em três partes principais: o corpo da célula, os dendritos e o axônio. Um neurônio recebe informações, ou impulsos nervosos, a partir dos dendritos. Estas informações são processadas no corpo celular e novos impulsos são transmitidos através do axônio para outros neurônios. A comunicação entre os neurônios, a sinapse, controla a transmissão dos impulsos, determinando o fluxo de informações com base na intensidade do sinal recebido [29, p. 36].

Figura 7.4: Representação de um neurônio biológico [30].

Por analogia ao parágrafo anterior, McCulloch e Pitts descreveram matematicamente um neurônio artificial como um modelo com vários terminais de entrada \(x_m\), representando os dendritos, e apenas um ponto de saída \(y_k\), como axônio (Figura 7.5). Para simular o comportamento das sinapses, cada entrada \(x_m\) é associada com um peso \(w_{km}\), sendo que o somatório representa a intensidade de sinais recebidos (\(v_k\)).

Figura 7.5: Representação matemática de um neurônio artificial [29, p. 36].

O sinal de resposta é estabelecido por uma função de ativação \(\varphi\) aplicada ao valor da soma ponderada, essa função apresenta comportamento limiar, Equação (7.1), em que a saída é \(0\) ou \(1\) conforme o valor limite (Figura 7.6). O modelo também pode incluir um bias (\(b_k\)) no somatório para aumentar o grau de liberdade da função de ativação e garantir que um neurônio não apresente saída nula mesmo que os sinais recebidos sejam nulos. O valor do bias é ajustado junto com os pesos sinápticos [29, p. 37].

\[y_k=\varphi(\upsilon_k)= \begin{cases} 1 \text{ se } \upsilon_k > 0 \\ 0 \text{ se } \upsilon_k \leq 0 \end{cases} \tag{7.1}\]

Figura 7.6: Função de ativação de limiar [29, p. 36]

O modelo proposto por McCulloch e Walter Pitts poderia realizar classificações em duas categorias, entretanto, os pesos precisavam ser ajustados manualmente pois não tinham a capacidade de aprender [23, p. 14]. Uma das primeiras discussões sobre regras de aprendizagem nas correções dos pesos sinápticos foi publicada em 1949 no livro de Donald Hebb “The Organization of Behavior” [29, p. 64]. No postulado de Hebb, apresenta-se que a conexão entre os neurônios é fortalecida cada vez que esta é utilizada, assim, os caminhos neurais no cérebro são continuamente modificados e formam agrupamentos.

A primeira rede neural com capacidade de aprender os pesos das categorias foi o Perceptron apresentado por Frank Rosenblatt em 1958 [29, p. 65]. O Perceptron tinha arquitetura semelhante à Figura 7.7, uma rede de camada única além da de entrada e de aprendizado supervisionado. Inicialmente, foram lançadas grandes expectativas sobre as possíveis aplicações do Perceptron, porém, as limitações logo começaram a ser destacadas, muitas descritas no livro de Marvin Minsky e Seymour Papert publicado em 1969. Uma das limitações é que o Perceptron de camada única realiza apenas a classificação de padrões linearmente separáveis em duas categorias, não podendo, por exemplo, representar o operador de lógica XOR, que não é linearmente separável [23, p. 14].

Figura 7.7: Arquitetura Perceptron [29, p. 47].

A imagem negativa sobre o Perceptron e suas limitações tecnológicas diminuiram a popularidade das redes neurais, o que reduziu o número de pesquisas na área até os anos 80 [23, p. 16]. O interesse pelas redes neurais começou a aumentar, principalmente, pelo uso da abordagem de processamento paralelo distribuído, como o aplicado no algoritmo de retropropagação (backpropagation) apresentado por Rumelhart, Hinton e Williams (1986). O backpropagation é o algoritmo mais utilizado para aprendizado profundo até hoje e foi crucial para o treinamento dos Perceptrons de múltiplas camadas (MLP, multi-layer Perceptron) [29, p. 184].

7.1.2.1 Rede MLP

Para que a rede de Perceptrons de múltiplas camadas pudesse aprender seria necessário a retropropagação dos erros de trás para frente entre as camadas, tornando possível a minimização da função custo. A necessidade do cálculo da derivada do erro implicou no aparecimento de funções de ativação diferentes da utilizada no modelo original do Perceptron, que não houvessem uma ativação abrupta, \(0\) ou \(1\), Figura 7.6 [29, p. 184]. Considerando que as funções de ativação são um dos elementos utilizados para a inclusão de não linearidade, ponto chave para que os modelos não se limitem aos padrões linearmente separáveis, a abordagem foi a incorporação de funções não lineares, mas “bem comportadas“, ou seja, que são “quase” lineares contínuas e deriváveis.

Como as funções de ativação são responsáveis pelo intermédio das respostas entre as camadas, deveriam ser considerados formatos não lineares que não alterassem de forma radical a resposta da rede. Os perfis que mais se aproximavam destes comportamentos são os das funções sigmóides: a tangente hiperbólica e a função logística [31].

A função sigmóide tem seu formato em S, em que nas extremidades da função tem um comportamento constante, o que fica evidente no gráfico da função logística (Figura 7.8). O parâmetro \(a\) da equação logística, Equação (7.2), permite parametrizar o comportamento da função, alterando a inclinação. Quanto maior o valor de \(a\), mais a função sigmóide se aproxima da função de limiar, Figura 7.6.

Figura 7.8: Função sigmóide [29, p. 39]

\[\varphi(\upsilon)=\frac{1}{1+\exp(-a\upsilon)} \tag{7.2}\]

Diferente da função limiar que assume valores \(0\) ou \(1\), a função logística tem resultados em um intervalo contínuo entre \(0\) e \(1\) [29, p. 40]. A função sigmóide também é diferenciável, enquanto que a função de limiar não. Uma forma anti-simétrica da sigmóide é a função tangente hiperbólica, Equação (7.3). A função tangente hiperbólica é definida no intervalo \(-1\) a \(1\), o que permite a função sigmóide assumir também valores negativos [29, p. 40].

\[\varphi(\upsilon)=\tanh(a\upsilon) \tag{7.3}\]

Ao se propor um método eficiente no treinamento dos Perceptrons de múltiplas camadas se tornou interessante a inclusão de uma ou mais camadas de neurônios ocultos entre a camada de entrada e de saída. A combinação de mais camadas permitiu que a rede fosse implementada para problemas mais complexos, não se restringindo às transformações lineares do modelo original do Perceptron. Por meio das camadas ocultas, é possível extrair de forma progressiva características importantes que definem os padrões de entrada [29, p. 184].

O neurônio matemático proposto inicialmente foi estendido para uma estrutura de conexões de elementos de processamento, os nós da rede. Os elementos foram organizados em camadas, e foram propostas diferentes configurações de conexões. Os formatos mais populares são definidos como uma arquitetura de rede neural, reconhecida pelo número de camadas da rede, número de nós em cada camada e tipo de conexão entre os nós.

A arquitetura da rede MLP é composta por uma camada de entrada que recebe o sinal, uma camada de saída que retorna o resultado, e entre elas um número arbitrário de camadas ocultas (Figura 7.9). Geralmente, a escolha do número de nós na camada de entrada e saída é direta. Por exemplo, em uma aplicação com imagens, o número de neurônios na camada de entrada pode corresponder ao número de pixels da imagem e o da camada de saída poderia ser apenas um único neurônio indicando a probabilidade de ser de fato o que se procura, a chance de um resultado positivo. Já o arranjo das camadas intermediárias não é tão simples, muitas vezes é definido empiricamente com base nas características dos dados de entrada e na complexidade do problema [32].

Figura 7.9: Arquitetura da rede MLP [29, p. 186].

Uma classificação comum das arquiteturas é com base no padrão de conexões, sendo identificadas duas classes principais: redes diretas (feedforward) e redes recorrentes (feedback) [29, p. 46]. O modelo MLP tem arquitetura do tipo feedforward, em que a propagação da informação ocorre em uma única direção e os nós de uma mesma camada não são conectados entre si. A saída de uma camada é usada como entrada na próxima, sem loopings, ou seja, não são enviadas de volta [29, p. 47].

Já nas tipologias recorrentes ocorre o feedback, um processo de realimentação, em que as saídas de nós são reinseridas como entradas em nós anteriores (Figura 7.10). O comportamento dos ciclos é dinâmico controlado por atrasos unitários [29, p. 49]. A ideia do modelo é estimular sinais em efeito cascata com dependência temporal.

Figura 7.10: Arquitetura rede recorrente [29, p. 49].

7.1.2.2 Backpropagation

Para explicar o algoritmo backpropagation no treinamento de redes neurais, utilizaremos um exemplo de aplicação de rede MLP para o reconhecimento de números. O código da rede é uma implementação do livro online “Neural Networks and Deep Learning” escrito por Michael Nielsen. Os dados de treinamento foram retirados do MNIST dataset, que contém mais de 60000 imagens escaneadas de números escritos juntamente com os rótulos de classificação. As informações foram coletadas pelo Instituto Nacional de Padrões e Tecnologia dos Estados Unidos (NIST), sendo que as imagens são em escala de cinza e de tamanho \(28\text{ x }28\) pixels como na Figura 7.11.

Figura 7.11: Um exemplo de número zero selecionado do MNIST dataset [33].

O conjunto de dados originais do MNIST é dividido em duas partes, uma que contém 60000 imagens para treinamento e a outra com 10000 imagens para a fase de testes, em que se avalia a acurácia da rede treinada para reconhecer os dígitos. No exemplo do autor Michael Nielsen, os dados de treinamento original também foram reorganizados em dois grupos, o primeiro com 50000 imagens que foram utilizados no treinamento e a outra parte, 10000 imagens, que foi reservada para a validação em que se definiu os hiperparâmetros da rede.

Considerando imagens de \(28 \text{ x } 28\) pixels, os dados de entrada foram definidos como um vetor \(x\) de dimensão \(784\), em que cada posição corresponde a um valor de pixel da imagem. Para o vetor \(y\) de saída da rede se estabeleceu a dimensão \(10\), em que cada posição faz referência a um dígito de \(0\) a \(9\). Assim, se uma entrada corresponde ao número \(3\) então a saída esperada será o vetor transposto na forma \(y(x)=(0,0,0,1,0,0,0,0,0,0)^T\). Com base no formato dos dados de entrada e saída da rede, o exemplo foi construído com uma rede MLP de três camadas como na Figura 7.12, com a primeira camada tendo \(784\) nós e a última camada com \(10\) nós. Na camada do meio, a camada oculta, utilizaremos \(30\) nós, mas vale destacar que o autor Michael Nielsen definiu o número de nós após alguns testes otimizando a escolha dos parâmetros da rede.

Figura 7.12: Rede MLP com uma camada oculta [34].

Os dados são retirados do arquivo zip “mnist.pkl.gz’”, subdivididos em treinamento, validação e de teste, e em seguida configurados no formato proposto da rede.

No Code Block 2, a rede é construída a partir do comando “Network([784, 30, 10], cost=QuadraticCost)”, em que cada argumento corresponde ao número de nós na camada. Os atributos da classe “Network” incluem o número de camadas “num_layers”, o número de nós em cada camada “sizes”, os pesos e bias iniciais, que são gerados aleatoriamente pelo método “default_weight_initializer()”, e a função custo “cost”. A função custo aplicada neste exemplo é definida na classe QuadraticCost, e foi usada a erro quadrático (Mean Squared Error - MSE).

class Network(object):
  def __init__(self, sizes, cost=QuadraticCost):
    self.num_layers = len(sizes)
    self.sizes = sizes
    self.default_weight_initializer()
    self.cost=cost

A seguir apresentaremos um resumo da teoria matemática do método backpropagation e para facilitar este processo utilizaremos a nomenclatura dos elementos de uma rede neural com base no livro “Introduction To The Theory Of Neural Computation” [34, p. 116]. No treinamento de uma rede como a da Figura 7.12 é apresentado um conjunto de treinamento \(\{\xi_k^\mu,\zeta_i^\mu\}\), em que cada padrão apresentado \((\mu=1, 2,\dots, p)\) corresponde a um par: entrada (\(\xi_k^\mu\)) e saída esperada (\(\zeta_i^\mu\)). Neste exemplo, o número de padrões no treinamento é \(p=50000\). O índice \(k\) na camada de entrada faz referência ao valor em cada nó da camada, e o índice \(i\) aos nós da camada da saída. A resposta final da rede é identificada como \(O_i\) e o sinal de saída da camada oculta é \(V_j\). A conexão entre a camada de entrada e a oculta é estabelecida pelos pesos \(w_{jk}\), e os pesos \(W_{ij}\) conectam a camada de saída com a intermediária.

O backpropagation é um método supervisionado em que o treinamento ocorre em duas fases [29, p. 163]. Na etapa forward, uma entrada é apresentada para a rede e de acordo com as conexões estabelecidas entre as camadas é propagado sucessivamente os sinais de respostas até a camada de saída, gerando um resultado que se espera ser o mais próximo do padrão. Cada nó de uma camada seguinte se conecta com todos os nós da camada anterior, sendo que o sinal recebido por este nó é uma ponderação dos pesos de todas as conexões. O sinal de entrada de cada nó recebe um bias e é passado para a próxima camada como uma resposta de uma função de ativação (\(g\)). A resposta de saída de um nó será denominada \(V_j\) se o sinal for para uma camada intermediária, ou \(O_i\) se for direcionado para a camada de saída.

Imagine que um nó (\(j\)) da camada intermediária recebe como entrada:

\[h_j^\mu=\sum_{k}w_{jk}\xi_k^\mu \tag{7.4}\]

e produz como resposta:

\[V_j^\mu=g(h_j^\mu)=g(w_{jk}\xi_k^\mu) \tag{7.5}\]

Assim, um nó na camada de saída recebe como entrada o sinal propagado:

\[h_i^\mu=\sum_kW_{ij}V_j^\mu=\sum_kW_{ij}g(\sum_kw_{jk}\xi_k^\mu) \tag{7.6}\]

gerando como resposta da saída da rede:

\[O_i^\mu=g(h_i^\mu)=g(\sum_kW_{ij}V_j^\mu)=g(\sum_kW_{ij}g(\sum_kw_{jk}\xi_k^\mu)) \tag{7.7}\]

No Code Block 3, a fase forward é representada pelo seguinte método:

feedforward(self, a):
  for b, w in zip(self.biases, self.weights):
    a = sigmoid(np.dot(w, a)+b)
  return a

No Code Block 4, a função de ativação é a função logística definida pelo método “sigmoid()” e a sua derivada é calculada no método “sigmoid_prime()”.

sigmoid(z):
  return 1.0/(1.0+np.exp(-z))
 
sigmoid_prime(z):
  return sigmoid(z)*(1-sigmoid(z))

Na segunda fase, backward, os pesos e bias são corrigidos camada a camada, no sentido da saída da rede até a sua entrada, em um processo iterativo de forma que a saída \(O_i\) fique cada vez mais próxima do padrão esperado \(\zeta_i\), reduzindo o erro [29, p. 163]. Uma forma de avaliar como o erro é reduzido em relação às alterações dos parâmetros é determinando uma função erro, ou custo, dependente dos pesos e bias. Conforme Equação (7.8), adotamos o erro quadrático (MSE) como função custo.

\[E[w]=\frac{1}{2}\sum_{\mu i}[\zeta_i^\mu-O_i^\mu]^2 = \frac{1}{2}[\zeta_i^\mu W_{ij}g(\sum_kw_{jk}\xi_k^\mu)] \tag{7.8}\]

No Code Block 5, a função custo (MSE) é apresentada no método “fn()” na classe “QuadraticCost”:

fn(a, y):
  return 0.5*np.linalg.norm(a-y)**2

A redução do erro envolve um processo de otimização, denominado descida em gradiente, em que se busca determinar os parâmetros (pesos e bias) que minimizam a função custo [33]. Neste método, a variação do erro pode ser escrita como derivadas parciais do erro em função dos pesos, compondo o vetor gradiente do erro. Como o vetor gradiente aponta no sentido de maior acréscimo do erro, a variação dos pesos é dada pelo negativo do gradiente, garantindo a redução mais rápida do erro. Assim, conforme Equação (7.9), a regra do gradiente descendente aplicada nas conexões entre a camada oculta e de saída pode ser escrita como:

\[\Delta W_{ij}=-\eta\frac{\partial E}{\partial W_{ij}}=\eta\sum_\mu[\zeta_i^\mu-O_i^\mu]g'(h_i^\mu)V_j^\mu=\eta\sum_\mu\delta_i^\mu V \tag{7.9}\]

\[\delta_i^\mu=[\zeta_i^\mu-O_i^\mu]g'(h_i^\mu) \tag{7.10}\]

A fórmula de modificações dos pesos é conhecida como regra delta e recebe o termo \(\eta\), a taxa de aprendizagem, para promover uma correção gradativa, sem alterações bruscas [33]. O termo \(g’\) se refere a derivada da função de ativação e surge na fórmula devido a derivação da função erro. A regra delta aplicada nas conexões entre a camada oculta e de entrada utiliza a regra da cadeia pois as derivadas são em relação aos pesos \(w_{jk}\), que se apresentam como dependência mais implícita ao erro. A correção dos pesos pode ser representada pela Equação (7.11):

\[\begin{split} \Delta w_{ij}&=-\eta\frac{\partial E}{\partial w_{jk}}=-\eta\sum_\mu\frac{\partial E}{\partial V_j^\mu}\frac{\partial V_j^\mu}{\partial w_{jk}}=\eta\sum_{\mu i}[\zeta_i^\mu-O_i^\mu]g'(h_i^\mu)W_{ij}g'(h_j^\mu)\xi_k^\mu \\ \\&=\eta\sum_{\mu i}\delta_i^\mu W_{ij}g'(h_j^\mu)\xi_k^\mu=\eta\sum_\mu\delta_j^\mu\xi_k^\mu \end{split} \tag{7.11}\]

\[\delta_j^\mu=g'(h_j^\mu)\sum_i\delta_i^\mu W_{ij} \tag{7.12}\]

Esta regra também pode ser estendida para redes com mais de uma camada oculta [31]. A regra delta generalizada para a m-ésima camada de uma rede pode ser descrita pela Equação (7.13):

\[\Delta w_{pq}^m=\eta\sum_\mu\delta_p^{m,\mu}V_q^{m-1,\mu} \tag{7.13}\]

\[ \delta_p^{m, \mu} = \begin{cases} \text{se m for a camada Output, } &[\zeta_p^\mu-O_p^\mu]g'(h_p^{m,\mu})\\ \text{senão, } &g'(h_p^{m,\mu})\sum_r\delta_r^{m+1,\mu}w_{rp}^{m+1} \end{cases} \tag{7.14} \]

A correção dos pesos ocorre considerando as conexões entre cada duas camadas, uma mais próxima da saída (\(p\)) e a outra mais interna (\(q\)). O vetor \(V_q\) representa o sinal de ativação recebido pela camada dos nós “\(p\)”, e quando o cálculo envolve a camada de entrada e a primeira camada oculta este vetor é o padrão de entrada (\(\xi_k^\mu\)). O fator delta (\(\delta\)) funciona como uma memória das respostas das camadas mais externas, ou seja, para modificar os pesos de trás para frente é necessário que as conexões das camadas mantenham memória das camadas que foram alteradas anteriormente. O algoritmo do backpropagation é utilizado na etapa de treinamento, Code Block 6, por meio do método “backprop()”:

backprop(self, x, y):
  nabla_b = [np.zeros(b.shape) for b in self.biases]
  nabla_w = [np.zeros(w.shape) for w in self.weights]
  # feedforward
  activation = x
  activations = [x] 
  zs = [] 
  for b, w in zip(self.biases, self.weights):
      z = np.dot(w, activation)+b
    zs.append(z)
    activation = sigmoid(z)
    activations.append(activation)
  # backward pass
  delta = (self.cost).delta(zs[-1], activations[-1], y)
  nabla_b[-1] = delta
  nabla_w[-1] = np.dot(delta, activations[-2].transpose())
  for l in range(2, self.num_layers):
    z = zs[-l]
    sp = sigmoid_prime(z)
    delta = np.dot(self.weights[-l+1].transpose(),delta) * sp
      nabla_b[-l] = delta
      nabla_w[-l] = np.dot(delta, 
      activations[-l-1].transpose())
  return (nabla_b, nabla_w)

Como destacado anteriormente, a primeira fase do backpropagation é o feedforward. Nesta etapa é recebido um padrão de entrada (\(x\)) e os pesos e bias inicializados aleatoriamente. Após o somatório das ponderações dos pesos e bias entre duas camadas, este valor é salvo no vetor “zs[ ]”, e o resultado da ativação deste valor é salvo em “activations[ ]”. A entrada da próxima camada é o sinal de ativação salvo em “actvivation”. Este processo ocorre da entrada até a camada de saída, salvando os sinais de ativação das camadas ocultas (\(V_j\)) em “activations[ ]”. Na fase backward pass, calcula-se primeiro o delta (\(\delta\)) a partir da resposta da camada de saída salva como o último elemento do vetor “activations[ ]” e do padrão de saída esperado (\(y\)). O valor de delta, neste caso, é calculado a partir do método “delta()” da classe “QuadraticCost” como o produto entre a diferença da resposta de saída de rede (\(a\)) e do valor esperado (\(y\)) com a derivada do sinal de ativação da última camada, conforme visto no Code Block 7:

delta(z, a, y):
  return (a-y) * sigmoid_prime(z)

Após o cálculo do primeiro delta, é determinado o incremento dos pesos (\(\Delta W_{ij}\)) entre a última camada e a camada oculta como o produto do delta (\(\sigma_i\)) pelo vetor de ativação (\(V_j\)) que a ultima camada recebeu como entrada. Os incrementos dos pesos são salvos no vetor “nabla_w[ ]”. Os deltas e incrementos dos pesos das camadas ocultas são obtidos de forma iterativa na estrutura de repetição. O cálculo do delta da camada m depende do somatório dos produtos do delta calculado anteriormente, da camada mais externa, com o vetor peso da camada m. O valor do somatório é multiplicado pela derivada do sinal de ativação da camada m. Em seguida, o valor do incremento dos pesos é obtido pelo produto do delta atual com o valor de ativação recebido pela camada m. Após realizar este mesmo processo para todas as camadas, a função retorna um vetor com os incrementos dos pesos com base em um padrão (\(\xi_k^\mu,\zeta_i^\mu\)), o que ocorre para todos os padrões de treinamento.

Para acelerar o processo de aprendizagem, em vez de atualizar os pesos cada vez que se apresenta um padrão, o autor Michael Nielsen sugere no seu exemplo a utilização do método gradiente descendente estocástico. A ideia é agrupar de forma aleatória os padrões de entrada formando o que ele chama de “mini-batch”. No método update_mini_batch(), a função backprop retorna o incremento do peso calculado para cada padrão dentro do agrupamento, e estes são somados em nabla-w até todo o agrupamento ser apresentado, e então os pesos e os bias são ajustados. Em seguida são apresentados os outros “mini-batch” até que todo o conjunto de treinamento seja utilizado, encerrando uma época de treinamento. Ou seja, em cada época, o conjunto de treinamento é subdividido em agrupamentos, e os pesos são atualizados apenas no final de apresentação de cada agrupamento como demonstrado no Code Block 8:

update_mini_batch(self, mini_batch, eta, lmbda, n):
  nabla_b = [np.zeros(b.shape) for b in self.biases]
  nabla_w = [np.zeros(w.shape) for w in self.weights]
  for x, y in mini_batch:
    delta_nabla_b, delta_nabla_w = self.backprop(x, y)
    nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
    nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
  self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)]
  self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)]

O treinamento ocorre a partir do método “SGD()”, sigla para descida do gradiente estocástico, em que são passados como parâmetros o conjunto de treinamento, o número de épocas, o tamanho do agrupamento “mini_batch_size” e a taxa de aprendizagem.

net.SGD(training_data,30,10,0.5, evaluation_data=test_data,monitor_evaluation_cost=True, monitor_evaluation_accuracy=True, monitor_training_accuracy=True, monitor_training_cost=True)

É no método “SGD()”, Code Block 10, que ocorre a subdivisão dos padrões de treinamento em agrupamentos “mini_batch”. Em seguida, é chamada a função “update_mini_batch()” para cada agrupamento até finalizar uma época, e isso se repete para todas as épocas.

SGD(self, training_data, epochs, mini_batch_size, eta,lmbda = 0.0 evaluation_data=None, monitor_evaluation_cost=False, monitor_evaluation_accuracy=False, monitor_training_cost=False, monitor_training_accuracy=False):
  for j in range(epochs):
    random.shuffle(training_data)
    mini_batches = [training_data[k:k+mini_batch_size] for k in range(0, n, mini_batch_size)]
    for mini_batch in mini_batches:
      self.update_mini_batch(mini_batch, eta, lmbda, len(training_data))
    print ("Epoch %s training complete" % j)

Dentro do método “SGD()” é possível configurar para avaliar o erro total e acurácia da rede após cada época de treinamento, tanto considerando os dados de treinamento quanto os dados de teste ou de validação. Para selecionar os dados de teste, eles devem ser passados como parâmetros no “evaluation_data”. Ao selecionar as opções “monitor_evaluation_cost” ou “monitor_training_cost” é chamado o método “total_cost()”, Code Block 11 que retorna a soma dos erros avaliados para todo o conjunto de dados.

total_cost(self, data, lmbda, convert=False):
  cost = 0.0
  for x, y in data:
    a = self.feedforward(x)
    if convert: y = vectorized_result(y)
    cost += self.cost.fn(a, y)/len(data)
    return cost

Após cada época se estabelece um conjunto de pesos e bias, e ao utilizar o método “feedforward()” são estes parâmetros que definem a resposta de saída da rede (\(a\)) para cada padrão de entrada (\(x\)). Ao comparar a resposta (\(a\)) com o valor esperado (\(y\)) dentro da função custo MSE, método “fn()” da classe “QuadraticCost”, quantifica-se o erro para cada padrão. O método “accuracy()”, Code Block 12, é utilizado dentro do “SGD()” quando se configura “monitor_evaluation_accuracy= True” ou “monitor_training_accuracy= True”. Esta função retorna a soma de resultados em que os valores de saída da rede corresponderam ao valor esperado (\(y\)). O sinal da rede é calculado pela função “feedforward()”, que é utilizada para cada valor (\(x\)) do conjunto de dados, seja de treinamento ou de avaliação

accuracy(self, data, convert=False):
  results = [(np.argmax(self.feedforward(x)), y) for (x, y) in data]
  return sum(int(x == y) for (x, y) in results)

Considerando que os valores do erro total e da acurácia são calculados para cada época, o método de treinamento “SGD()” retorna quatro vetores dentro de uma tupla, cada um com o número de posições correspondentes ao número total de épocas. Assim, se o treinamento ocorrer em \(30\) épocas, então a primeira lista da tupla terá \(30\) elementos correspondentes ao custo total dos dados de avaliação no final de cada época.

return evaluation_cost, evaluation_accuracy,training_cost, training_accuracy

Os resultados salvos podem ser plotados em gráficos para avaliar visualmente o desempenho da rede. Um gráfico muito comum para acompanhar o treinamento da rede é o de custo de treinamento, principalmente, porque o aprendizado é guiado pela minimização desta curva. Na Figura 7.13, apresenta-se a curva de custo para uma configuração que utiliza o conjunto total de treinamento (50000 imagens) e com 30 épocas. Entretanto, não é indicado ter apenas este gráfico como base para estabelecer os hiperparâmetros da rede, como a taxa de aprendizagem e o número de épocas de treinamento. Por exemplo, a Figura 7.14 também se refere a uma função de custo, mas para uma outra configuração de treinamento, que utiliza apenas 1000 imagens para treinamento e 100 épocas.

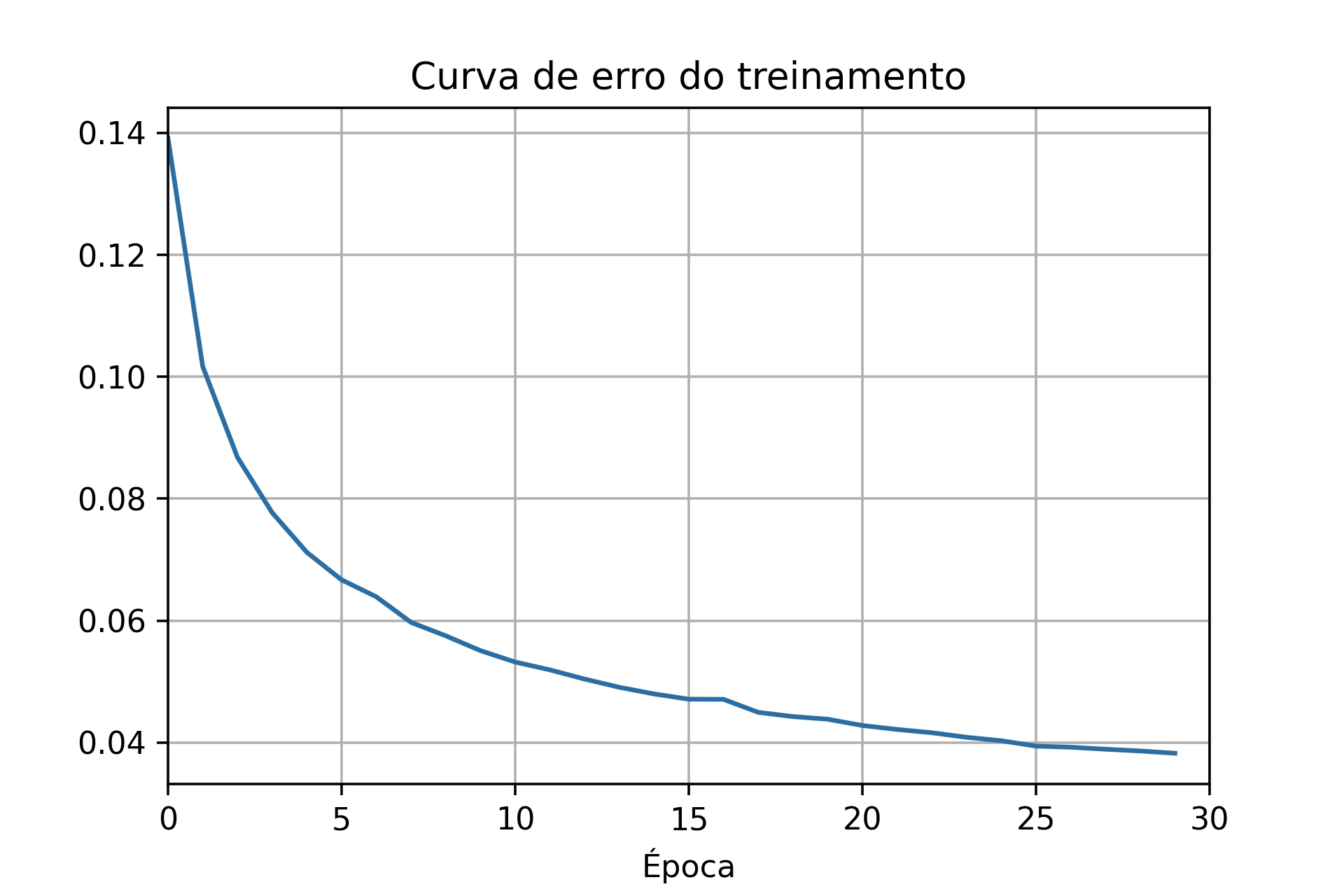
Figura 7.13: Curva de custo no treinamento com 30 épocas e 50000 imagens.

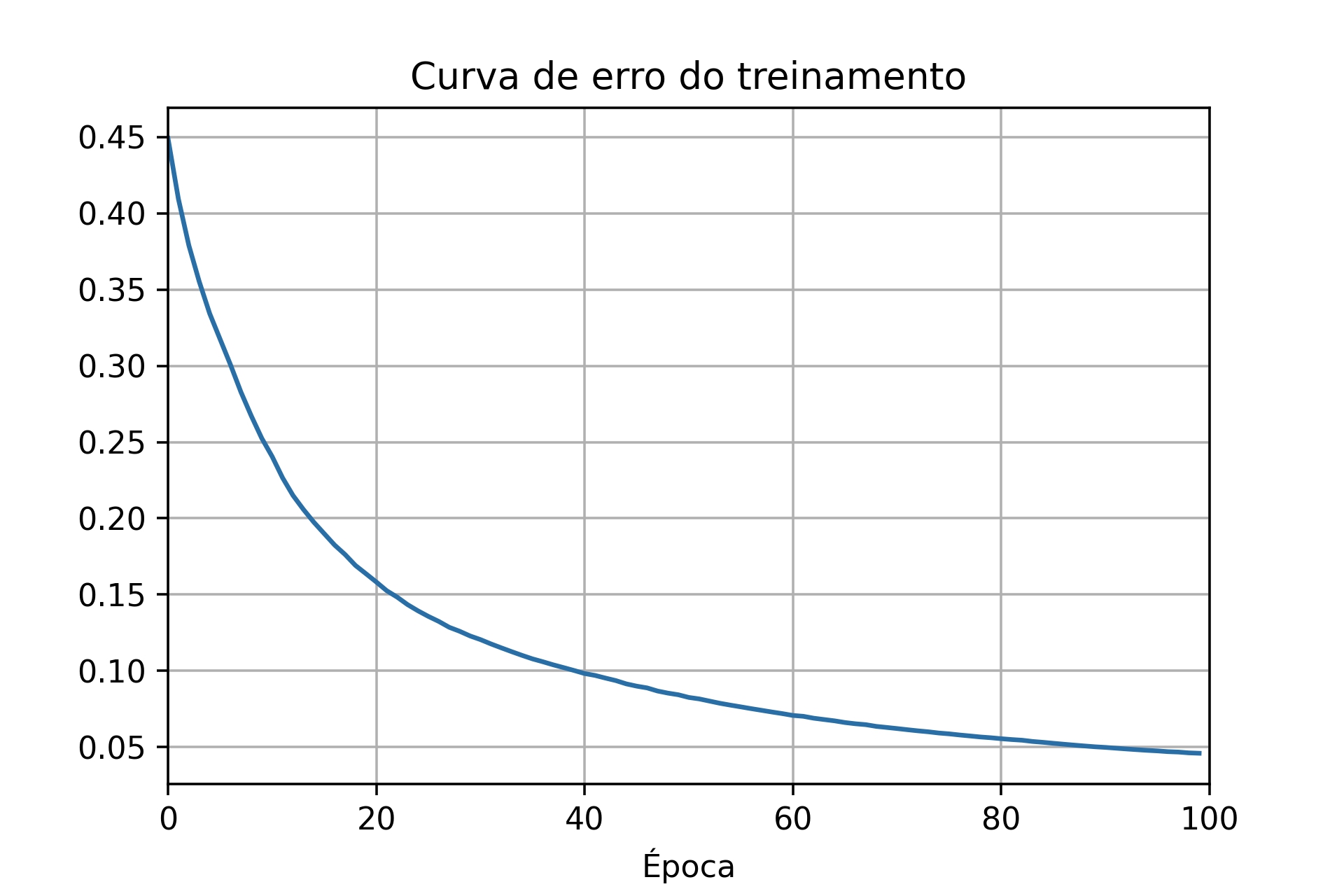
Figura 7.14: Curva de custo no treinamento com 100 épocas e 1000 imagens.

No fim do treinamento, as duas redes apresentaram erros na mesma ordem de grandeza, mas a capacidade de reconhecer números é bem diferente entre as duas. Esta diferença pode ser percebida ao comparar os gráficos de acurácia (Figuras 7.15 e 7.16) considerando tanto os dados de treinamento quanto os de validação. O resultado do treinamento com todo o conjunto de dados mostra que a acurácia da rede para os dados de validação é bem próxima do resultado para os valores de treinamento, uma diferença de \(1\%\). Já para a situação que utilizou apenas 1000 dados de treinamento, as curvas de acurácia para os dados de validação e de treinamento estão mais afastadas, apresentando uma diferença próxima de \(14\%\).

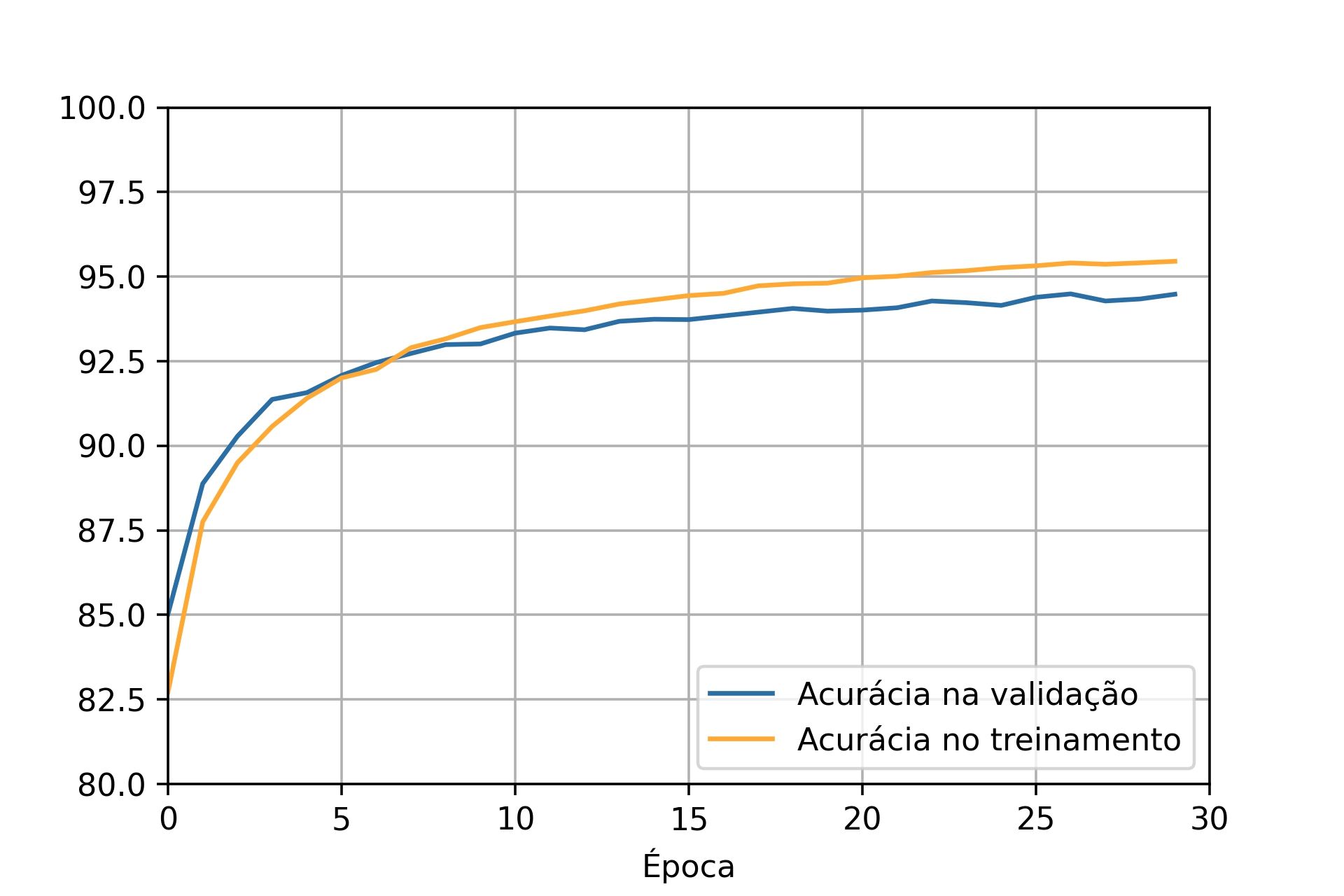
Figura 7.15: Curvas de acurácia para rede treinada com \(30\) épocas e \(1000\) imagens.

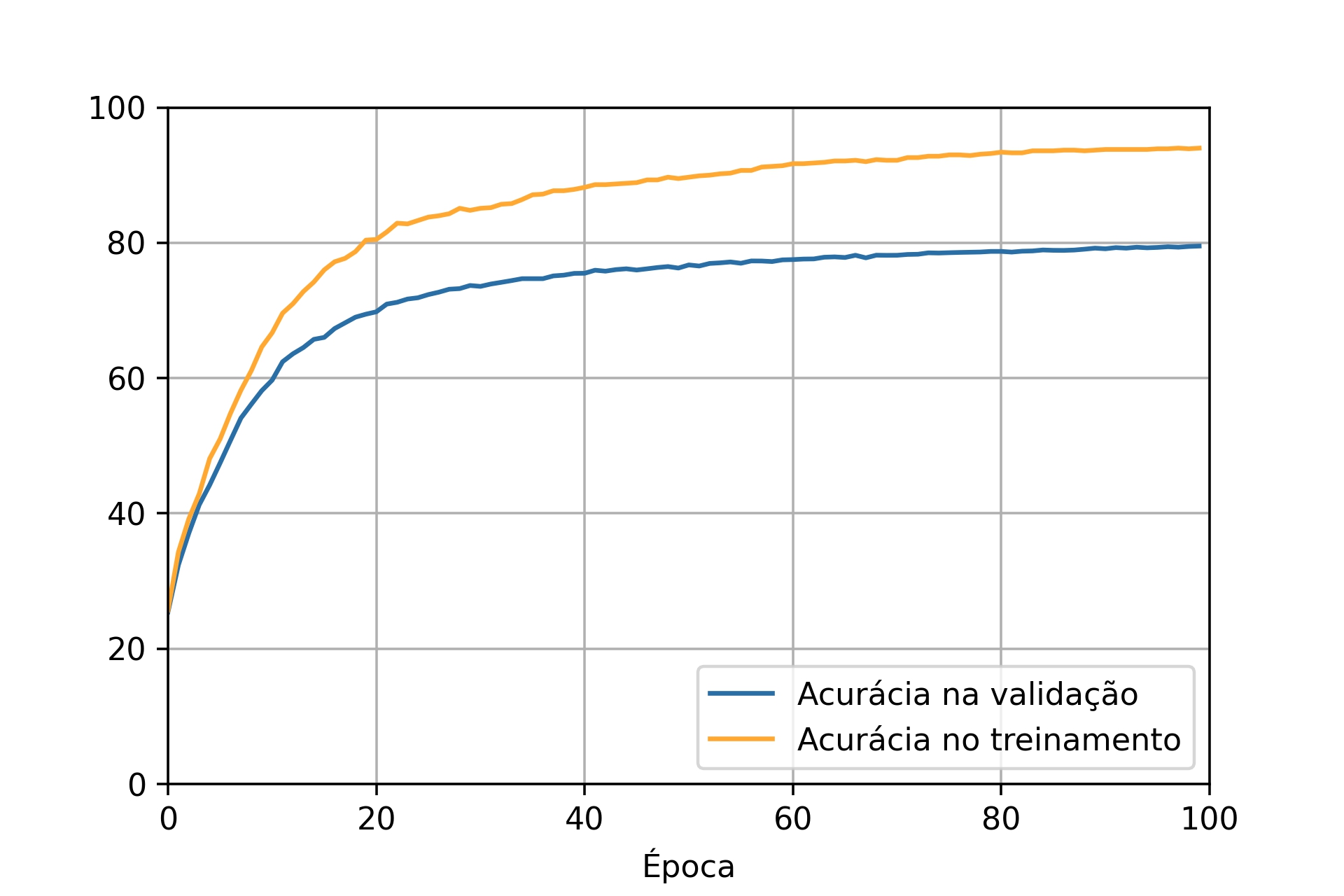
Figura 7.16: Curvas de acurácia para rede treinada com \(100\) épocas e \(1000\) imagens.

Ao observar apenas a curva de erro se imagina que a rede esteja aprendendo até o final do treinamento, visto que o erro continua diminuindo. Entretanto, ao analisar as curvas de acurácia se identifica que a acurácia determinada pelos dados de validação aumenta rapidamente até uma determinada época, próximo de 40 no segundo caso, e em seguida fica estagnada. Assim, após a 40ª época, a rede não está mais aprendendo a generalizar para os dados de validação, está ocorrendo overfitting, ou seja, o treinamento não está melhorando a capacidade da rede. Mesmo que a acurácia do treinamento esteja aumentando depois desta época, pode ser que a rede esteja apenas decorando os dados de treinamento, pois não está mais se atendo apenas às informações gerais necessárias para reconhecer os números de forma geral [33].

Os casos mais comuns de se ocorrer overfitting é quando o número de dados do treinamento é muito baixo, como neste segundo caso com apenas 1000 imagens. Nesta situação, a rede tem poucos exemplos para extrair informações gerais, precisando muitas vezes aumentar o número de épocas de treinamento para que se alcance um desempenho mínimo. Quanto maior o número de épocas pode ser mais evidente o efeito de overfiting, por isso se recomenda observar quando a acurácia da validação começa a estagnar e a ficar muito distante da curva de treinamento [33].

Observar o comportamento da acurácia da validação é um dos métodos para definir até quando a rede deve ser treinada, ou seja, o número de épocas. Os dados de validação ajudam no teste de diferentes configurações de hiperparâmetros da rede, como épocas de treinamento, taxa de aprendizado e número de nós. Só depois de definir estes parâmetros e treinar a rede que se recomenda a utilização dos dados de teste para verificar realmente a acurácia da rede, utilizando dados que ela ainda não teve contato [33]. Um teste com dados não conhecidos permite verificar se os parâmetros da rede podem ser aplicados em casos mais gerais ou se enquadram apenas em particularidades dos dados treinados. Por esta razão, na maioria dos casos os dados são divididos em três conjuntos - treinamento, validação e teste.

7.2 Redes neurais convolucionais (CNN)

A área de deep learning tem conseguido ótimo desempenho em aplicações, principalmente, pelo desenvolvimento da área e pelo aumento do poder computacional e da quantidade de dados disponíveis [35, p. 431]. Um dos tipos de redes neurais, conhecida como Redes Neurais Convolucionais (Convolutional Neural Networks - CNN), também tem conseguido resultados ótimos, um dos motivos pelos quais foram adotadas com relevância pela área de visão computacional, substituindo muitas das técnicas antigas, que por utilizarem algoritmos mais “estáticos” eram difíceis de serem aplicados em diferentes áreas.

7.2.1 Blocos de construção de uma CNN

Nas redes neurais mais simples usamos basicamente neurônios e conexões entre eles para realizar a construção de um modelo. Já as redes neurais convolucionais contam com algumas estruturas a mais que são o porquê de sua eficiência no trabalho com imagens. Veremos elas a seguir.

7.2.1.1 Operador de convolução

A operação que dá nome a rede, a convolução, é uma operação realizada entre duas funções como explicada em Convolução, na seção de Filtros Digitais. No nosso caso, como estamos trabalhando com imagens, usamos a convolução discreta.

Um ponto importante a se frisar é que matematicamente o que chamaremos de convolução é na verdade uma correlação, sendo que as duas são quase idênticas, a não ser pelo fato de que na convolução giramos o filtro (kernel) em \(180^\circ\). A única vantagem que ganhamos em girar o filtro antes da operação é que ganhamos a propriedade comutativa, o que é útil matematicamente para derivação de provas mas não é importante na implementação de deep learning [23, p. 332].

Na literatura e nas bibliotecas de deep learning, incluindo CNN’s, se tornou comum chamar as duas operações de convolução [23, p. 333], então também usaremos essa convenção, utilizando a convolução sem girar o filtro, assim, uma correlação.

Relembrando do Tópico de Convolução, a fórmula da correlação discreta é dada por:

\[g(x,y)=w(x,y)\bigstar f(x,y)=\sum_{s=-a}^a\sum_{t=-b}^bg(s,t)f(x+s,y+t) \tag{7.15}\]

Onde \(w\) é o nosso filtro (kernel) e \(f\), a nossa imagem. E relacionado a ela temos a fórmula da convolução:

\[g(x,y)=w(x,y)\ast f(x,y)=\sum_{s=-a}^a\sum_{t=-b}^bg(s,t)f(x-s,y-t) \tag{7.16}\]

Como podemos perceber observando as duas equações, essas operações são bem simples, sendo basicamente uma soma de produtos. Na Figura 7.17, temos uma representação de um passo da convolução, onde podemos observar a seguinte operação:

\[ \text{w}\text{*f}\left(0,0\right)\text{=}\sum_{s}^{}\sum_{t}^{}\text{w}\left(s,t\right)\text{f}\left(0+s,0+t\right)\,\text{=}\, \text{+w}\left(-1,-1\right)\text{f}\left(-1,-1\right)\text{+w}\left(-1,0\right)\text{f}\left(-1,0\right)\text{+w}\left(-1,1\right)\text{f}\left(-1,1\right) \text{+w}\left(0,-1\right)\text{f}\left(0,-1\right)\text{+w}\left(0,0\right)\text{f}\left(0,0\right)\text{+w}\left(0,1\right)\text{f}\left(0,1\right) \text{+w}\left(1,-1\right)\text{f}\left(1,-1\right)\text{+w}\left(0,1\right)\text{f}\left(0,-1\right)\text{+w}\left(1,1\right)\text{f}\left(-1,-1\right) =\,1\cdot0+0\cdot0+\left(-1\right)\cdot0 +2\cdot0+0\cdot2+\left(-2\right)\cdot1 +1\cdot0+0\cdot9+\left(-1\right)\cdot3 =0\,-2-3\,=\,-5 \tag{7.17} \]

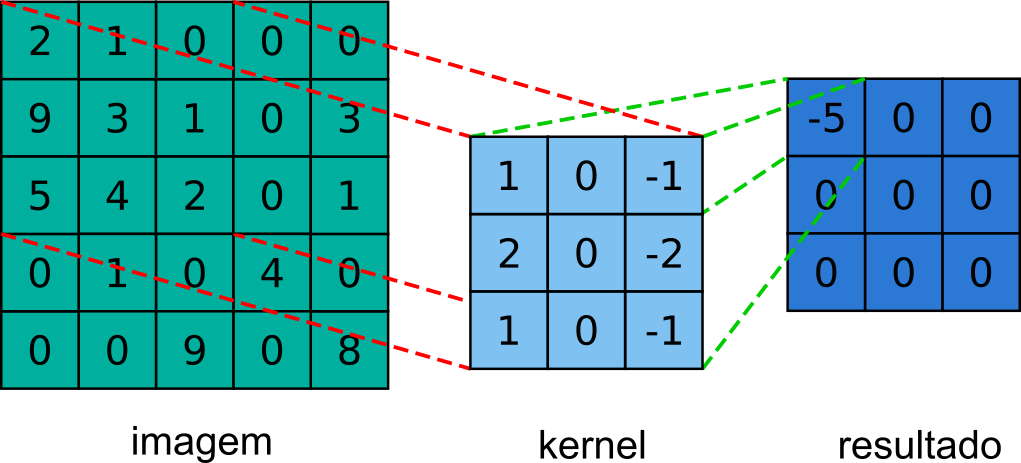
Figura 7.17: Convolução de uma imagem de tamanho 5x5 com um kernel de tamanho 3x3 e seu respectivo resultado.

O exemplo anterior, Figura 7.17, foi bem simples, mas sabemos que em várias aplicações não teremos a imagem de entrada representada por apenas uma matriz (configurando uma imagem em tons de cinza) mas em grande parte das vezes estaremos utilizando imagens que contém três dimensões, ou seja, teremos uma imagem no modelo RGB, onde estarão presentes três matrizes, cada uma representando um canal de cor. Na Figura 7.18, há um exemplo de convolução em imagens RGB, podemos ver que agora nosso kernel é também formado por três matrizes. Uma coisa importante a se notar é que o número de camadas do filtro têm que ser igual ao número de canais da imagem para que a operação de convolução possa ser feita.

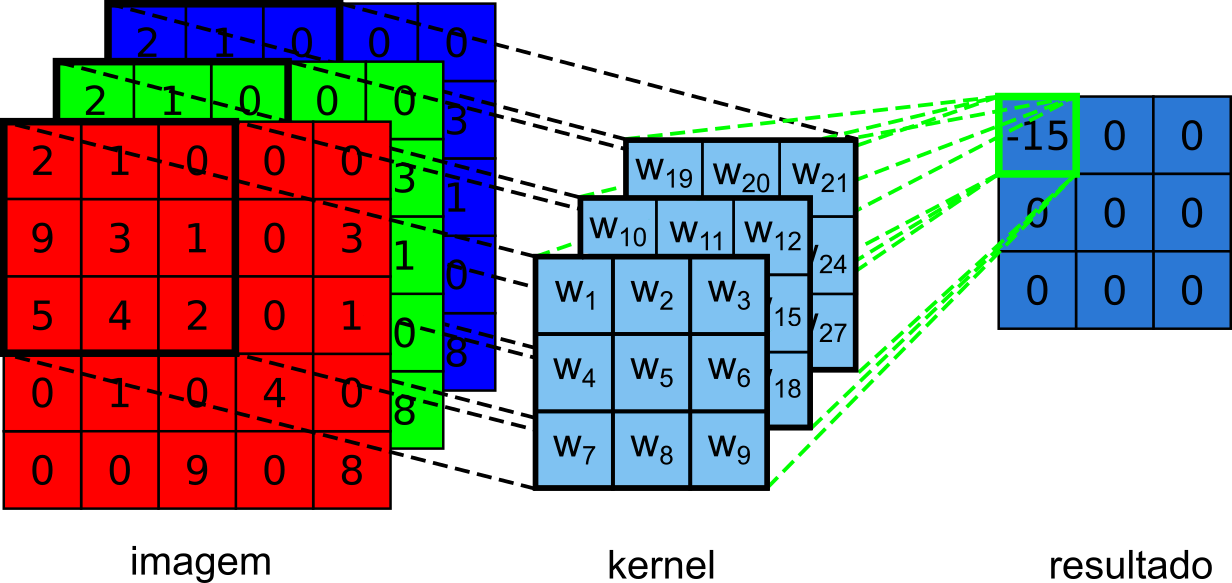
Figura 7.18: Convolução de uma imagem de tamanho 5x5x3 com um kernel de tamanho 3x3x3 e seu respectivo resultado.

Na Figura 7.19, temos uma representação de uma camada de convolução com mais de um filtro. Para cada um dos filtros temos uma saída e, consequentemente, temos no resultado final um conjunto de dados onde o número de camadas de profundidade (também conhecidas como feature map, ilustrada pelas três matrizes em azul) corresponderão ao número de filtros aplicados a entrada. Essa saída então pode ser enviada para frente na rede, passando por mais convoluções e tendo mais características extraídas.

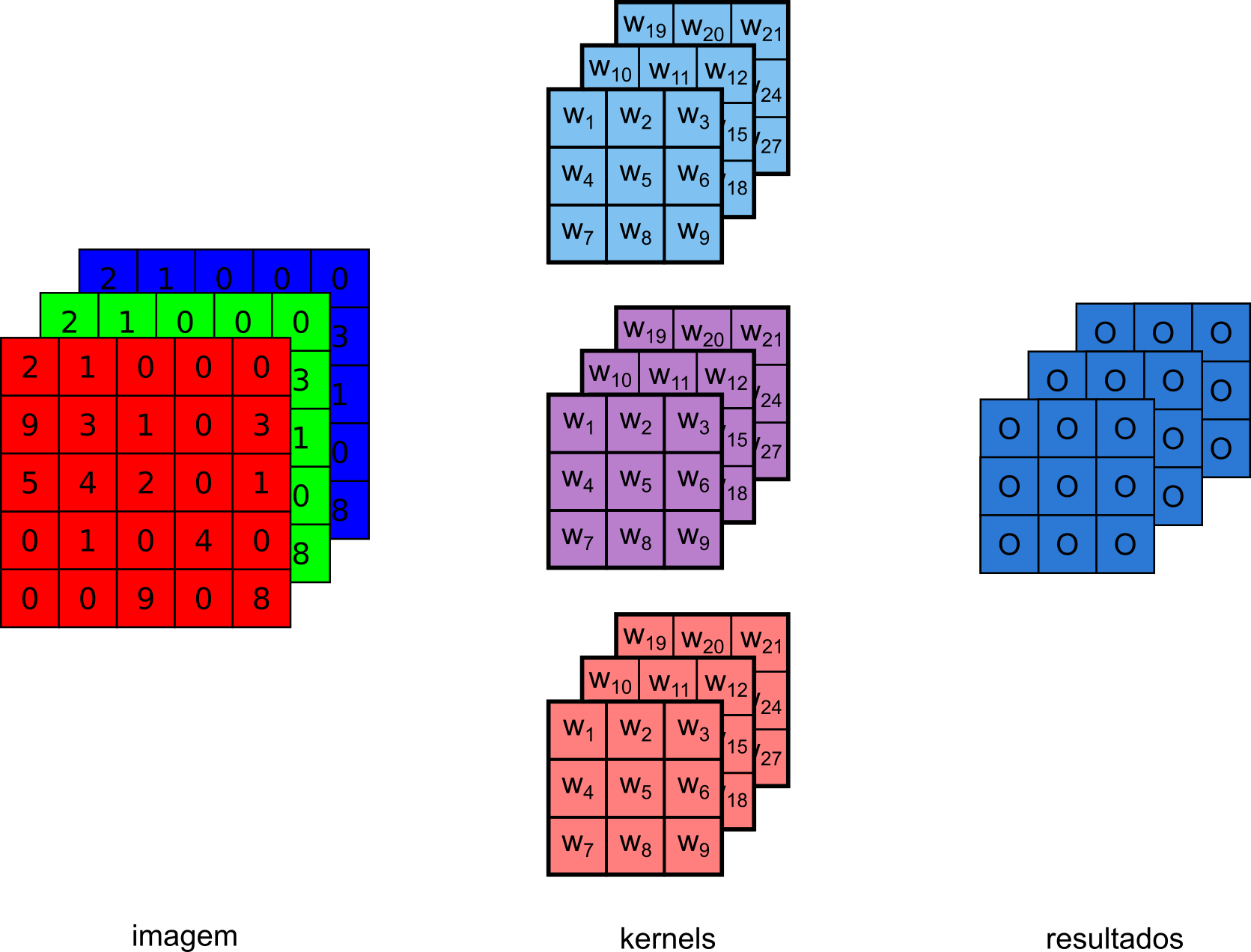
Figura 7.19: Convolução com múltiplos kernels.

Os dois exemplos anteriores, Figuras 7.17 e 7.19, também servem para nos mostrar uma das características da convolução que a fazem ser uma boa escolha para se trabalhar com imagens, chamamos essa característica de iterações esparsas (também conhecida como conectividade esparsa) [23, p. 335]. Esse atributo evidencia o fato de que cada unidade da saída, ou pixel, é conectada a somente uma fração das unidades de entrada. No nosso exemplo anterior, cada saída é conectada a uma região dos 243 pixels de entrada, 9x9x3. Isso é muito útil, pois nossa imagem pode ter milhões de pixels, e usando kernels de tamanhos menores, conseguiremos detectar pequenas características, como bordas, quinas, etc [23, p. 335]. Nas camadas de convolução, os valores que a rede deverá aprender são os valores presentes nos filtros, então dessa maneira teremos menos parâmetros para aprender e armazenar. Em uma rede neural simples, como vimos no tópico Rede MLP, uma imagem na entrada significa que cada pixel seria conectado a cada neurônio na próxima camada, assim, resultaria em uma rede excessivamente grande.

Uma outra característica importante é o de compartilhamento de parâmetros, já que o mesmo filtro é aplicado a diferentes regiões da imagem utilizando os mesmos valores, diferentemente de uma rede neural sem camadas de convolução, onde temos uma matriz com pesos que são usados para somente uma conexão. O compartilhamento de parâmetros nos proporciona uma outra característica, que é a invariância à translação, isso quer dizer que se movemos a posição de um objeto na imagem de entrada, sua representação também será movida na imagem resultante [23, p. 339].

7.2.1.1.1 Padding

Nos exemplos de convolução, Figuras 7.17 e 7.19, vemos que conforme aplicamos o kernel na imagem de entrada, o tamanho da imagem de saída é reduzido. De fato, ao convolucionar uma imagem de tamanho \(m \text{ x }n\) com um filtro de tamanho \(k_m \text{ x } k_n\) a imagem resultante terá uma altura de \(m - k_m + 1\) e um comprimento de \(n - k_n + 1\). Esse tipo de convolução, onde a imagem resultante é menor geralmente é chamada de “valid” (válida).

Se queremos a imagem de saída com o mesmo tamanho da imagem de entrada, temos que adicionar mais linhas e colunas em nossa imagem, isso é conhecido como padding. Nesse caso, utilizamos a fórmula \(m + 2p - k_m + 1\) e \(n + 2p - k_n + 1\) onde \(p\) representa o padding. Por exemplo, nas Figuras anteriores, Figuras 7.17 e 7.19, se quiséssemos uma saída de igual tamanho a da entrada, teríamos que utilizar um padding de \(6 + 2p - 3 + 1 = 6 \Rightarrow p = 1\).

7.2.1.1.2 Stride

Os exemplos de convolução que vimos anteriormente utilizavam passos de deslocamento de um em um, mas podemos também utilizar passos maiores, pois assim reduzimos o custo computacional ao realizar esses passos intervalados. Isso, claramente, tem um impacto no resultado final, diminuindo sua resolução, mas em casos onde não precisamos extrair características delicadas isso se torna uma boa opção [23, p. 348].

Quando utilizamos um valor de stride maior que um, isso também afetará o tamanho da saída, que será governada pela seguinte relação [36, p. 184]:

\[\frac{m+2p-k_m}{s}+1 \ \times \ \frac{n+2p-k_n}{s}+1 \tag{7.18}\]

Onde \(m\) e \(n\) são as dimensões da imagem, \(p\) é o padding, \(k_m\) e \(k_n\) são as dimensões do kernel e \(s\) é o stride. Na Figura 7.20 temos um exemplo com os passos (Figuras 7.20(a-d)) de uma convolução com \(\text{stride} = 2\) utilizando um kernel de tamanho \(3 \text{ x } 3\) sobre uma imagem de tamanho \(5 \text{ x } 5\) e \(\text{padding} = 0\).

Figura 7.20: Representação de uma convolução com \(\text{stride} = 2\). Adaptado de [37].

7.2.1.2 Pooling

Essa é uma camada muito importante, que tem como objetivo realizar a subamostragem (subsampling) da imagem para reduzir seu tamanho, e, consequentemente, diminuir o total de memória, processamento e parâmetros necessários, além de refrear o risco de overfitting [35, p. 442] [36, p. 187] [38, p. 114].

Como nas camadas de convolução cada unidade da saída é conectada a uma região de entrada, então, também devemos levar em consideração o tamanho, stride e padding. Mas, diferentemente da convolução, o “kernel”, ou, em outras palavras, a região que nos conectará com a entrada, não terá pesos mas apenas realiza uma operação, sendo as mais comuns o máximo ou a média [35, p. 442].

Na Figura 7.21, temos um exemplo de max pooling, onde podemos ver seu funcionamento em passos (Figuras 7.21(a-d)). Este exemplo utiliza uma região de \(2 \text{ x } 2\), o que é muito comum [36, p. 187], com \(\text{stride}=1\).

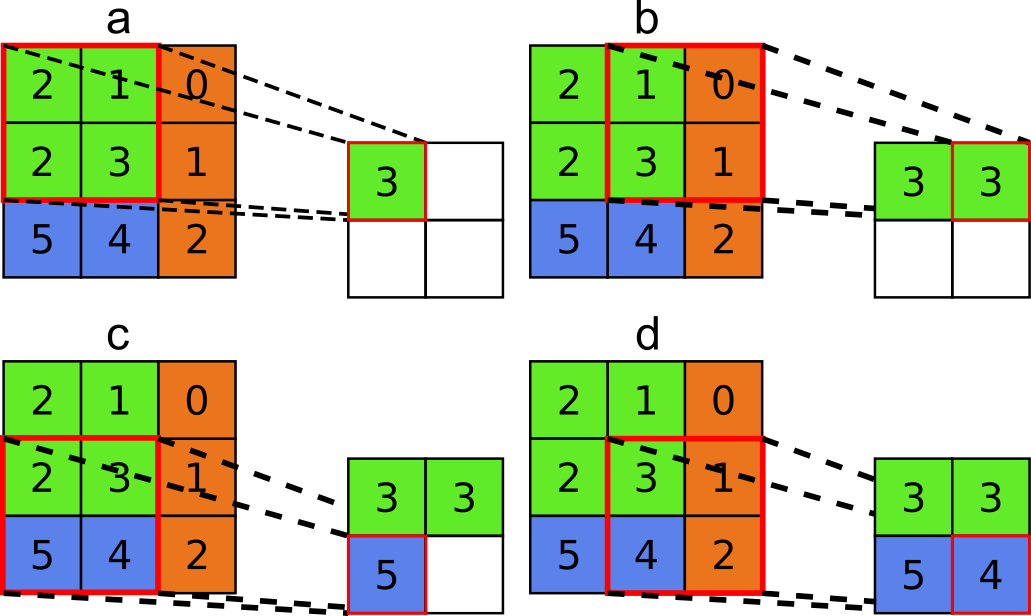
Figura 7.21: Exemplo de aplicação do max pooling.

Na Figura 7.22, temos outro exemplo de max pooling, mas desta vez realizado com uma entrada de maiores dimensões, podemos ver que a operação é realizada em cada uma das camadas do objeto de entrada, e que sua saída contém o mesmo número de camadas da entrada, sendo que é isso que tipicamente ocorre nesse tipo de operação [35, p. 443].

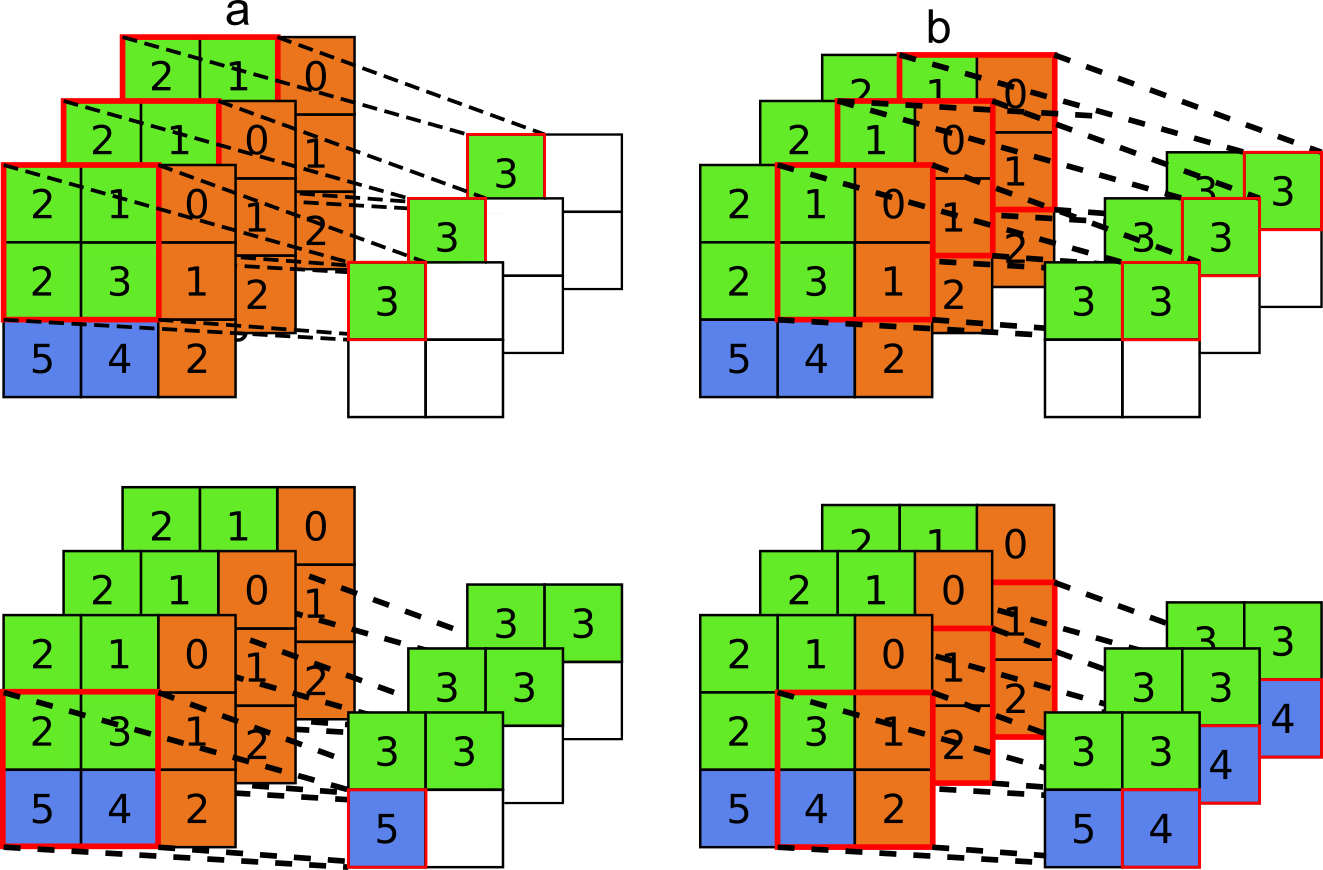
Figura 7.22: Exemplo da aplicação de max pooling em uma imagem com mais dimensões, uma RGB por exemplo.

Apesar do pooling ser uma técnica muito difundida, podemos encontrar redes onde seus autores preferiram não utilizar pooling para realizar a subamostragem, mas utilizarem camadas de convolução com valores de stride e padding maiores para conseguir essa redução de dimensão [38, p. 117] [36, p. 188]. Essa maneira de trabalhar foi proposta por Springenberg et al. em seu artigo “Striving for Simplicity: The All Convolutional Net” de 2014, onde demonstram que mesmo redes sem camadas de pooling podem ter resultados bons em diferentes bases de dados, como o CIFAR-10 e ImageNet.

7.2.1.3 Camadas totalmente conectadas

As CNN’s geralmente tem várias camadas de convolução seguidas por camadas de ReLU que por sua vez são seguidas por camadas de pooling, e esse processo vai diminuindo as dimensões \(m \text{ x }n\) e aumentando a profundidade, ou seja, a quantidade de camadas de características (conhecida como feature maps) [38, p. 119] [35, p. 446]. Na Figura 7.23, temos uma representação desse processo através da topologia da rede. Ao final dessa rede temos uma quantidade grande de camadas com as características extraídas da imagem de entrada, e precisamos utilizar essas informações. Nessa mesma Figura, podemos ver que no final temos camadas totalmente conectadas (fully connected) que é uma rede neural regular, uma MLP [38, p. 119].

Figura 7.23: Típica arquitetura de uma rede neural convolucional [35, p. 447].

Na Figura 7.24, temos a representação da utilização dessas informações abstraídas da imagem, onde recebemos o resultado das camadas de convolução, um bloco de dados de \(5 \text{ x } 5 \text{ x } 40\) da última camada de pooling, que é então planificado (flattened) em um vetor contínuo de uma dimensão e dado como entrada a uma rede MLP que, ao final, tem uma camada Softmax que faz a classificação da imagem de entrada.

Figura 7.24: Camada totalmente conectada [38, p. 120].

7.2.2 Por que usar convoluções

Até agora entendemos os blocos de construção das CNN’s e os motivos pelos quais são usados. Devemos saber que a convolução não é apenas usada por ser mais eficiente no tratamento de imagens, mas também pela inspiração em nosso próprio sistema visual.

7.2.2.1 Córtex visual

Como as próprias redes neurais, as CNN’s foram bio-inspiradas em estudos sobre o córtex visual do cérebro que começaram a ocorrer desde 1980 [35, p. 431], principalmente a partir dos trabalhos de David H. Hubel e Torsten Wiesel, onde foram realizados experimentos em animais, que permitiu eles deduzirem o funcionamento da estrutura do córtex visual.

De uma maneira simplificada, os sinais de luz recebidos pela retina são transmitidos ao cérebro através do nervo óptico, após isso chegam ao córtex visual primário que é formado principalmente por dois tipos de células [23, p. 365]:

• Células simples: essas células têm comportamentos que podem ser representados por funções lineares em uma imagem em uma pequena área conhecida como campo receptivo [23, p. 365] [35, p. 432]. Esse tipo de célula inspirou as unidades detectoras mais simples nas CNN’s.

• Células complexas: também respondem a características da imagem, como as células simples, mas são invariantes a posição, ou seja, não fazem grande distinção de onde a característica aparece. Esse tipo de célula inspirou as unidades de pooling, que veremos mais adiante [23, p. 365].

Anatomicamente, quanto mais nos aprofundamos nas camadas do cérebro, mais camadas análogas à convolução e pooling são passadas, e encontramos células mais especializadas que respondem a padrões específicos sem serem afetadas por transformações na entrada. Sendo que até chegar nessas camadas mais profundas, é realizado uma sequência de detecções seguidas de camadas de pooling [23, p. 365].

7.2.3 Redes CNN’s clássicas

7.2.3.1 LeNet

Após estudar os principais blocos de construção de uma rede convolucional (CNN) - camada de convolução (convolutional layer), camada de redução (pooling layer) e camadas totalmente conectadas (fully connected layer) - torna-se mais fácil comparar as arquiteturas CNN’s e perceber que mesmo com as diferenças elas apresentam um padrão na combinação das camadas. Normalmente, as arquiteturas CNN’s possuem uma sequência intercalada de camada de convolução, seguida por uma camada pooling, que se repete até a ponta da rede onde se encontram algumas camadas totalmente conectadas com estrutura semelhante às redes MLP. Esta estrutura básica pode ser vista na Figura 7.25.

À medida que são realizadas as operações ao longo da rede se percebe que os mapas ficam cada vez menores e que as camadas ficam mais profundas, ou seja, aumentam a quantidade de mapas em uma mesma camada. Como a camada de saída geralmente se apresenta como um vetor de probabilidades para as classes de predição, existe uma transição da representação dos dados em mapas para vetor, a partir do processo de flatten, que ocorre antes da primeira camada totalmente conectada.

Figura 7.25: Rede Convolucional LeNet - A entrada é uma imagem de um número escrito à mão e a saída um vetor com a probabilidade para cada um dos dez dígitos de 0 à 9 [39, p. 250].

A rede LeNet foi uma das primeiras CNN’s que demonstrou potencial de aplicação em visão computacional. A rede foi criada por Yann LeCun em 1998 com propósito de reconhecimento de números manuscritos. A LeNet foi posteriormente adaptada para reconhecer dígitos para os depósitos em máquinas ATM, e ainda existem caixas eletrônicos que executam o código desenvolvido por Yann e seu colega Leon Bottou [39, p. 248]. A rede também foi amplamente utilizada para reconhecimento de dígitos do dataset do MNIST [35, p. 449], este dataset foi abordado no Tópico Backpropagation.

Na Figura 7.25, consideramos como entrada uma imagem padrão do MNIST, de tamanho \(28 \text{ x } 28\) pixels e com um canal em escala de cinza. No esquema geral da rede LeNet (Figura 7.26), temos uma visão mais clara da combinação das camadas, em que após a camada de entrada existem duas camadas convolucionais, intercaladas com duas camadas de pooling e na ponta três camadas totalmente conectadas.

Cada camada de convolução utiliza um filtro \(5 \text{ x } 5\) e uma função de ativação sigmóide. A primeira camada de convolução tem seis canais ou mapas, enquanto a segunda tem 16. A operação de pooling envolve um filtro \(2 \text{ x } 2\) que calcula a média, por isso é identificada como “AvgPool”, e utiliza \(\text{stride}=2\) para que cada mapa da camada anterior tenha uma redução pela metade ao longo da largura e da altura, descartando \(75\%\) das ativações. O tamanho das três camadas totalmente conectadas (fully conected) são respectivamente, 120, 84, e 10. A última camada, “FC(10)”, corresponde ao número possível de classes, neste caso, 10 em razão dos dígitos de 0 à 9. A função de ativação na última camada é uma função gaussiana.

Figura 7.26: Esquema geral das camadas na rede LeNet - Esquema da rede LeNet com a sequência de camadas convolucionais (“Conv”), pooling (“AvgPool”) e camadas totalmente conectadas (“FC”) [39, p. 252].

Para compreender os efeitos de cada camada sobre o conjunto de dados, apresentamos na Tabela 7.1, as dimensões das saídas de cada camada. Comentamos que de um bloco de convolução para o outro ocorre um aumento do número de canais (C) de 6 para 16, entre as camadas de pooling estes valores não são alterados, pois o processo só reduz a largura (W) e altura (H) dos canais. Nas camadas totalmente conectadas, as dimensões são reduzidas até se obter o tamanho do número de classes.

É comum nas redes CNN’s que a quantidade de canais praticamente dobre depois de uma camada pooling visto que ocorre uma redução pela metade nas dimensões dos mapas. Assim, é possível aumentar o número de mapas, tornando mais sensível a identificação de características de baixo nível, como bordas e texturas, sem aumentar drasticamente o número de parâmetros e recursos computacionais [39, p. 258]. Como a primeira camada de convolução aplica \(\text{padding}=2\), os mapas mantêm na saída a mesma dimensão que a imagem original (\(28 \text{ x } 28\)), entretanto na segunda camada não se tem o padding, o que reduz em 4 pixels a largura e altura dos mapas.

Tabela 7.1: Configurações, parâmetros e informações das camadas na LeNet - Resumo das configurações das principais camadas da LeNet, como o número de canais e tamanho dos filtros. Apresentação de uma estimativa do número de parâmetros e da quantidade de memória para treinar a rede.

Layer	Canais - C	Tamanho - H e W	Filtro - K	Memória (kB)	Parâmetros
Inputs	1	28
Convolucional 1	6	28	5	18	156
Avg Pooling 1	6	14	2	5	0
Convolucional 2	16	10	5	6	2416
Avg Pooling 2	16	5	2	2	0
Flatten	400			1.6	0
Full Connect 1	120			0.5	48120
Full Connect 2	84			0.3	10164
Full Connect 3	10			0.04	850
Total				33	61706

Ao longo dos anos surgiram variações deste modelo e a diferença mais evidente entre as redes é o número de camadas, que foi aumentando ao longo dos anos tornando as redes mais profundas. Ao aumentar o número de camadas se percebia que o desempenho das redes tendia a melhorar, entretanto foram surgindo algumas limitações. Quanto maior a quantidade de dados, mais memória computacional é exigida, sendo que esta capacidade depende dos requisitos do hardware.

Para avaliar a quantidade de memória utilizada no treinamento da rede LeNet vamos utilizar um cálculo aproximado com base na quantidade de elementos de saída em cada camada. O número de elementos é multiplicado pela quantidade de bytes necessária para armazenar cada elemento [40]. Considerando que os dados em ponto flutuante ocupam \(32 \text{ bits}\), logo \(4 \text{ bytes}\) por elemento, para facilitar a visualização dos resultados é utilizado a medida kilobyte (kB), e por isso foram divididos pelo fator 1024 já que \(1 \text{ kB} = 1024 \text{ B}\). Na Equação (7.19), exemplificamos o cálculo da quantidade de memória para a primeira camada de convolução da rede LeNet:

\[ \begin{split} \text{Quantidade de memória necessária }& = \text{CxHxW}\\ &= 6 \text{ x } 28 \text{ x } 28\\ &= 4704 \text{ elementos da saída}\\ &= 4704 \text{ x }4 \text{ bytes} = 18816 \text{ bytes}\\ &= 18.38 \text{ kilobytes} \end{split} \tag{7.19} \]

O parâmetro C identifica o número de canais ou mapas da camada e o termo H e W, a altura e largura do elemento de saída da camada, respectivamente. Como identificado na Equação (7.19) e na Tabela 7.1, a quantidade aproximada de memória para a primeira camada seria \(18 \text{ kB}\), e no total para a rede \(33 \text{ kB}\). As primeiras camadas tendem a precisar de mais memória devido a maior dimensão (W e H) dos canais [40].

Aumentar o número de camadas também exige que mais parâmetros sejam considerados, o que afeta tanto o tempo de treinamento quanto o seu desempenho, pois se não ocorrer uma otimização adequada dos parâmetros pode ser maior a probabilidade de ocorrer overfitting [38, p. 230]. Para determinar aproximadamente a quantidade de parâmetros relacionados com cada camada considerou-se os pesos relacionados aos filtros de cada mapa, calculados como o produto entre as dimensões do filtro (\(\text{K x K}\)), a quantidade de canais do elemento de entrada e a quantidade de canais de saída da camada [40]. Considerou-se também como parâmetros, os bias associados a cada canal de saída. Nas camadas totalmente conectadas, o número de parâmetros é determinado como produto da quantidade de elementos de entrada com a quantidade de elementos da saída da camada somado com o número de bias. A Equação (7.20) exemplifica os cálculos para a primeira camada de convolução:

\[ \begin{split} \text{Número de Pesos} &= \text{C}_\text{saída} \text{ x } \text{C}_\text{saída} \text{ x } \text{K} \text{ x } \text{K}\\ &= 6\text{ x }1 \text{ x } 5 \text{ x } 5\\ &= 150\\\\ \text{Número de Bias} &= 6\\\\ \text{Número de parâmetros} &= \text{Número de Pesos} + \text{Número de parâmetros}\\ &= 150 + 6\\ &= 156 \end{split} \tag{7.20} \]

Considerando que o filtro na primeira camada é de tamanho \(5\text{ x }5\), que a entrada só apresenta um canal e que são 6 canais na camada de convolução, a primeira camada de convolução considera aproximadamente 156 parâmetros. Na Tabela 7.1, também está a quantidade de parâmetros relacionados com cada camada e o total aproximado de parâmetros para a rede LeNet é 61706. À medida que aumenta o número de canais na camada de convolução mais parâmetros são necessários. De maneira geral, a maior parte dos parâmetros se deve às camadas totalmente conectadas devido ao maior número de conexões [40].

7.2.3.2 AlexNet

Atualmente existem várias arquiteturas de redes CNN’s utilizadas para aplicações na visão computacional. A evolução destas redes pode ser compreendida a partir dos resultados da competição ImageNet Large Scale Visual Recognition Challenge (ILSVRC). O principal objetivo da competição era avaliar algoritmos para detecção de objetos e classificação de imagens. A primeira edição da competição, em 2010, envolvia 1,2 milhões de imagens para o treinamento, sendo 1000 categorias de objetos. Nos dois primeiros anos de competição as redes CNN’s ainda não tinham sido as primeiras colocadas, porém a partir de 2012 os modelos CNN’s começaram a liderar a competição [41]. O progresso das redes pode ser avaliado com base na taxa de erro dos modelos que em sete anos caiu de aproximadamente \(26\%\), no segundo ano da competição, para \(2.3\%\) na última edição da competição em 2017 [40], como apresentado no gráfico da Figura 7.27.

Figura 7.27: Taxa de erro dos modelos de melhor desempenho na competição ImageNet - O desempenho dos modelos na competição ImageNet Large Scale Visual Recognition Challenge (ILSVRC) era avaliado principalmente pela taxa de erro. No gráfico são apresentados os modelos que venceram em cada edição da competição, que ocorreu de 2010 à 2017, e também redes que se tornaram populares como a VGG [40].

Para conhecer um pouco dos diferentes modelos de redes CNN’s e perceber algumas diferenças, e estruturas que tiveram bom desempenho e permaneceram em modelos mais atuais, destacaremos a seguir quatro arquiteturas que ficaram bastante conhecidas e tiveram destaque na competição. A rede AlexNet foi a primeira CNN que venceu a competição ImageNet, no ano de 2012 com uma taxa de erro de \(16.4\%\). A rede VGG não liderou a competição em 2014, porém é um dos modelos com bastante popularidade e que apresentou uma estrutura em blocos estabelecidos com base em regras. No ano de 2014, a CNN GoogLeNet que venceu a competição foi o ponto de partida para as redes Inceptions. A rede Residual (ResNet) em 2015 além de aproveitar as técnicas de maior desempenho das outras redes também implementou uma abordagem que possibilitou aumentar para mais de 100 camadas.

A rede AlexNet foi desenvolvida por Alex Krizhevsky, Ilya Sutskever, e Geoffrey Hinton [35, p. 450]. Esta rede é bem semelhante a LeNet-5, porém apresenta mais camadas. Por ser uma rede mais profunda, exigindo maior quantidade de memória, a rede original precisou ser distribuída entre dois GPU’s de 3 GB de forma física [42]. Desta forma, a rede foi desenhada como na Figura 7.27, com uma estrutura de fluxo de dados duplo para que cada GPU recebesse metade do modelo.

Figura 7.28: Arquitetura da rede AlexNet - representada como a combinação de duas redes idênticas, pois originalmente o treinamento ocorreria com a distribuição dos dados entre duas GPU’s [42].

Como esquematizado na Figura 7.28, a AlexNet tem 5 camadas de convoluções, sendo as três primeiras intercaladas por camadas pooling. A diferença mais visível entre as arquiteturas AlexNet e LeNet são as três camadas de convolução a mais na rede AlexNet, que estão seguidas uma depois da outra sem camada pooling entre elas. Como as imagens de entrada são maiores que do dataset MNIST abordado na rede LeNet, os filtros de convolução na entrada são maiores (\(11\text{ x }11\)) e se utiliza \(\text{stride} = 4\). Na segunda camada de convolução, os filtros têm tamanho \(5\text{ x }5\), e nas demais camadas de convolução se utilizam filtros \(3\text{ x }3\).

Com a descoberta de que as funções de ativação ReLU’s nas camadas de convolução e que o maxpooling melhoram o desempenho das redes, a maioria dos modelos foram construídos utilizando estes artifícios [39, p. 250]. Os filtros maxpooling de tamanho \(3\text{ x }3\) e \(\text{stride} = 2\) reduzem a dimensão dos canais com base no maior valor do campo de recepção. Com exceção da primeira camada, todas as demais camadas de convolução têm padding para que a dimensão dos canais não seja alterada após as convoluções.

As três últimas camadas são totalmente conectadas e apresentam respectivamente os tamanhos, 4096, 4096 e 1000. A camada de saída tem dimensão 1000 devido ao número de classes possíveis da competição ImageNet e a função de ativação é a Softmax.

Figura 7.29: Comparação das redes AlexNet e LeNet. (a) é a Rede LeNet e (b), a Rede AlexNet. Estes esquemas gerais das camadas apresentam que a principal diferença das redes é que a AlexNet é mais profunda, com três camadas de convolução a mais do que a LeNet [39, p. 261].

O mesmo padrão para as dimensões dos elementos de saída das camadas visto em LeNet é visto na Tabela 7.2 para a rede AlexNet. Enquanto o tamanho dos canais diminui entre uma camada de convolução para outra, a quantidade de canais cresce, sendo 96 na primeira, seguida por 256, 384, 384 e 256. Após o processo de flatten, a dimensão das camadas é reduzida até se estabelecer o tamanho do vetor de classes de predição.

Ao comparar a quantidade de memória e o número de parâmetros aproximados como foi descrito no Tópico de LeNet observa-se que certamente a quantidade de memória exigida aumenta e o número de parâmetros também. Os cálculos aproximados indicam que enquanto a memória necessária para o treinamento da rede LeNet seria de \(33 \text{ kB}\), na AlexNet seria aproximadamente \(3\text{ GB}\). O número de parâmetros calculados para LeNet foi 62 mil e para AlexNet 62 milhões. Mas de maneira geral, nos dois modelos, as primeiras camadas demandam mais memória, enquanto que as camadas totalmente conectadas precisam de mais parâmetros.

Tabela 7.2: Configurações, parâmetros e informações das camadas na AlexNet - Resumo das configurações das principais camadas da AlexNet, como o número de canais e tamanho dos filtros. Apresentação de uma estimativa do número de parâmetros e da quantidade de memória para treinar a rede.

Layer	Canais - C	Tamanho - H e W	Filtro - K	Memória (kB)	Parâmetros
Inputs	3	227
Convolucional 1	96	55	11	1134	35
Max Pooling 1	96	27	3	273	0
Convolucional 2	256	27	5	729	615
Max Pooling 2	256	13	3	169	0
Convolucional 3	384	13	3	254	885
Convolucional 4	384	13	3	254	1327
Convolucional 5	256	13	3	169	885
Max Pooling 3	256	6	3	36	0
Flatten	9216			36	0
Full Connect 1	4096			16	37753
Full Connect 2	4096			16	16781
Full Connect 3	1000			4	4097
Total				3090	62378

7.2.3.3 VGG

A rede VGG foi construída dentro do grupo Visual Geometry Group (VGG) na Universidade de Oxford pelos pesquisadores Karen Simonyan e Andrew Zisserman [39, p. 265]. Até agora vimos que as redes LeNet e AlexNet apresentam a sua estrutura em duas partes principais, uma com as camadas iniciais contendo uma combinação de camadas convolucionais e pooling, e na outra parte estão as camadas totalmente conectadas (fully conected) na ponta da rede. Nestas redes, geralmente, é necessário selecionar individualmente vários parâmetros, por exemplo, nas camadas de convolução, selecionam-se o número de canais, tamanho dos filtros, do padding e do stride. Na camada pooling, os hiperparâmetros são o tamanho do filtro e do stride. Em geral, estas duas redes não apresentam um guia geral de como selecionar os parâmetros, o que torna mais complexo desenhar novas redes e que sejam mais profundas.

O que se destacou na VGG em relação aos dois modelos anteriores é a introdução de princípios para estabelecer a estrutura da rede, o que permitiu a construção de modelos mais profundos [39, p. 265]. Outro aspecto característico da VGG é a estrutura em blocos na parte da rede com as camadas convolucionais, em que cada bloco apresenta camadas convolucionais em sequência e na ponta uma camada pooling. Enquanto o modelo AlexNet, na Figura 7.30, apresenta 5 camadas convolucionais, a VGG apresenta cinco blocos com número variável de camadas de convolução, mas que em geral os primeiros blocos apresentam menos camadas. Da mesma forma que a AlexNet, na ponta da rede estão as três camadas totalmente conectadas, com dimensões também iguais nos dois modelos, e uma função de ativação Softmax na saída.

Na Figura 7.30, está a representação da arquitetura VGG com 16 camadas, em que os primeiros dois blocos apresentam duas camadas convolucionais e os três últimos blocos possuem três camadas convolucionais. As camadas de convolução dobram de tamanho a cada bloco, sendo que cada camada no primeiro bloco tem 64 canais, no seguinte 128 e assim por diante até 512 no último bloco. A utilização da função de ativação ReLu na camada de convolução e pooling pelo valor máximo são estratégias que apresentaram bom desempenho na AlexNet e continuaram em outros modelos, como no VGG.

Os principais princípios de design da VGG estabelecem que todos os filtros de convolução são \(3\text{ x }3\) com \(\text{stride} = 1\) e \(\text{padding} = 1\), e que os filtros maxpooling são \(2\text{ x }2\) com \(\text{stride} = 2\). Após cada camada pooling, o número de canais dobra na camada de convolução. A ideia de fixar o tamanho dos filtros convolucionais partiu da percepção de que a combinação de dois filtros \(3\text{ x }3\) apresenta um campo receptivo equivalente a um filtro \(5\text{ x }5\), e que três filtros \(3\text{ x }3\) equivalem a um de \(7\text{ x }7\) [38, p. 212]. Fixando o tamanho dos filtros e seus \(\text{stride} = 1\) e \(\text{padding} = 1\) estabelece que a dimensão dos canais não se altere entre as camadas convolucionais, o único hiperparâmetro que precisa ser otimizado é a quantidade de camadas em cada bloco.

Ao utilizar filtros \(3\text{ x }3\), que são menores, porém, em maior quantidade que os utilizados na AlexNet (\(11\text{ x }11\) e \(5\text{ x }5\)), inclui-se mais não linearidade, permitindo que a rede aprenda mais características de baixo nível [38, p. 212]. Aumentando a profundidade da rede com mais camadas de convolução são incluídas mais funções não lineares de ativação. Mesmo sendo redes mais profundas, esta estratégia de utilizar filtros menores diminui o número de parâmetros. Considerando que duas camadas em sequência tem C canais cada uma, ao utilizar dois filtros \(3\text{ x }3\), o número total de parâmetros é \(2\text{ x }3\text{ x }3\text{ x }\text{C}^2 = 18\text{C}^2\), que é menor ao comparar à situação de um único filtro \(5\text{ x }5\) com \(25\text{C}^2\) parâmetros [40].

Certamente dobrar o número de canais entre os blocos deve fazer com que o número de parâmetros cresça rapidamente, e por isso se padronizou os filtros maxpooling para que se reduza as dimensões dos canais pela metade. Controlando o número de ativações que passam para as próximas camadas é possível manter aproximadamente constante o número de operações. Avaliando superficialmente que o número de operações é dado como a quantidade total de multiplicações e adições, podemos calcular para cada camada como produto de quatro parâmetros [40]: tamanho do filtro (\(\text{K x K}\)), as dimensões do canais de entrada (\(\text{H x W}\)), a quantidade de canais de entrada (\(\text{C}_{\text{entrada}}\)) e canais na saída (\(\text{C}_{\text{saída}}\)):

\[ \begin{split} \text{Número de operações} &= \text{Número de elementos de saída x Operações por elemento de saída}\\ &= (\text{C}_{\text{saída}} \text{ x H x W}) \text{ x } (\text{C}_{\text{entrada}} \text{ x K x K})\\ &= (2\text{C x HW}) \text{ x } (\text{2C x 3 x 3})\\ &= 36 \text{HWC}^2 \end{split} \tag{7.21} \]

No caso de duas camadas de convolução com filtros \(3\text{ x }3\) e separadas por um pooling, com redução pela metade da dimensão dos canais (\(\text{2H x 2W} \rightarrow \text{H x W}\)) e dobrando o número de canais (\(\text{C} \rightarrow \text{2C}\)), a quantidade de pesos aumenta de \(9\text{C}^2\) para \(36\text{C}^2\), porém o número de operações se mantêm em \(36\text{HWC}^2\).

Figura 7.30: Comparação das redes VGG e AlexNet - Comparação das redes VGG e AlexNet com base na estrutura geral das camadas. Enquanto a parte final das redes é semelhante em relação às camadas totalmente conectadas, a VGG se diferencia por ser mais profunda e apresentar um padrão das camadas convolucionais organizadas em blocos [40]

7.2.3.4 GoogLenet e Inception

Ao acompanhar a evolução das CNN’s podemos perceber que a principal estratégia para aumentar o desempenho na classificação das imagens foi aumentar o número de camadas que guardam os pesos das redes. As redes AlexNet e VGG-16 foram desenvolvidas com 8 e 16 camadas, respectivamente. À medida que as redes se tornavam mais profundas surgiu o dilema de como tornar os algoritmos mais eficientes, visto que mais camadas significava maior quantidade de parâmetros e operações, exigindo maiores recursos computacionais. Comparando as redes na Figura 7.31 é possível verificar a acurácia das redes, a quantidade de parâmetros e o número de operações. Verifica-se que para a rede VGG-16 alcançar resultados melhores que a rede AlexNet foi necessário mais do que duplicar a quantidade de parâmetros, de aproximadamente 65 milhões na AlexNet para um pouco mais que 130 milhões na VGG-16.

Na competição da ImageNet de 2014, um grupo de pesquisa da Google liderado por Christian Szegedy propôs a arquitetura GoogLeNet que deveria ao mesmo tempo garantir boa performance e ser mais eficiente que os modelos existentes [35, p. 452]. O modelo não só ganhou a competição como atendeu os seus requisitos, pois mesmo sendo uma rede com 22 camadas, mais que a VGG-16, precisou de 12 vezes menos parâmetros, 13 milhões em vez de 138 milhões [38, p. 217].

Figura 7.31: Gráfico da evolução das redes neurais CNN’s - O desempenho das redes é avaliado pela acurácia versus o número de operações necessárias para uma única etapa forward. O raio dos círculos é proporcional ao número de parâmetros, sendo que a legenda no canto inferior direito indica uma referência de \(5\text{ x }10^6\) à \(155\text{ x }10^6\) [43].

Para compreender a rede GoogLenet podemos dividi-la em três partes (Figura 7.32), na primeira parte, as camadas da entrada são semelhantes às redes AlexNet e VGG, na segunda parte, são os blocos inceptions característicos desta rede, e a última parte se refere a estrutura de classificação. A primeira parte contém dois blocos com uma sequência de camadas convolucionais intercaladas com pooling \(3\text{ x }3\). No primeiro bloco, tem apenas uma camada de convolução \(7\text{ x }7\), com \(\text{stride} = 2\) e \(\text{padding}= 3\), e uma camada pooling com \(\text{stride} = 2\). Ao final destas duas camadas, o elemento tem 64 canais e teve uma redução por 4 em sua dimensão (H e W). No segundo bloco, são duas camadas de convolução, a primeira com filtro \(1\text{ x }1\) e 64 canais e a segunda \(3\text{ x }3\) com 192 canais, sendo que apenas o pooling \(3\text{ x }3\) na ponta do bloco altera as dimensões dos canais pela metade.

O principal papel destes dois blocos é reduzir de maneira considerável as dimensões da imagem, visto que a maior parte da memória exigida se deve às primeiras camadas [40]. Considerando que nesta etapa ocorre uma redução em 8 vezes das dimensões da imagem, uma entrada \(224\text{ x }224\) ao se reduzir para \(28\text{ x }28\) utilizará aproximadamente \(7.5 \text{ MB}\) de memória enquanto a mesma redução no VGG-16 precisa de \(42.9 \text{ MB}\), quase \(6\) vezes mais que a GoogLenet [40]. Também ao passar para as próximas camadas uma imagem de menor dimensão também se reduz o número de operações e a quantidade de parâmetros para treinar a rede.

Figura 7.32: A estrutura geral da rede GoogLenet pode ser dividida em três partes: Parte A - Semelhante a AlexNet e LeNet, contém uma sequência de camadas convolucionais e pooling para reduzir as dimensões da imagem; Parte B - Módulos Inceptions separados por camadas pooling; Parte C - Camada de pooling global e uma Full Conect para classificação [38, p. 224].

Outra técnica para tornar a rede mais eficiente foi incluir uma camada de AvgPool global antes da camada de classificação [35, p. 455]. Nos modelos CNN’s anteriores era comum incluir um flattering para converter os dados em um vetor, perdendo a informação espacial, para ser compatível com as camadas totalmente conectadas que faziam a classificação. Estas últimas camadas acabam sendo as responsáveis pela maior parte dos parâmetros. No modelo VGG-16, por exemplo, as 3 camadas totalmente conectadas geram aproximadamente \(123.6\) milhões de parâmetros, quase \(90\%\) dos parâmetros totais [40].

Em vez de adotar o flattering, o GoogLenet utiliza um filtro de média de mesma dimensão do elemento de entrada, retornando a média dos mapas para cada posição do vetor. Como o vetor de saída já tem um tamanho reduzido é necessário incluir apenas uma camada totalmente conectada com as \(1000\) classes. Como a camada de média global não precisa de parâmetros, e considerando que retorna um vetor \(1024\), são necessários aproximadamente \(1\) milhão de parâmetros na camada totalmente conectada, \(100\) vezes menos que na VGG [40]. Na última camada, assim como no VGG, associa-se uma ativação Softmax, enquanto nas camadas de convolução é a ReLu.

Já foi comentado sobre a primeira parte e a última da rede GoogLenet, a seção intermediária que estudaremos inclui os módulos Inceptions que se tornaram elementos característicos das redes mais modernas intituladas Inceptions. Cada módulo se assemelha aos blocos do VGG, em que estão presentes algumas camadas convolucionais em sequência e na ponta uma camada pooling. No caso do VGG, viu-se que para reduzir o número de hiperparâmetros se fixou o tamanho dos filtros em \(3\text{ x }3\), e o parâmetro variável ficou sendo o número de camadas convolucionais. A ideia dos Inceptions (Figura 7.33) é não se preocupar nem com tamanho dos filtros e nem com o número de camadas no módulo, pois cada módulo consiste em uma combinação de filtros de diferentes tamanhos arranjados de uma forma fixa [38, p. 217].

Figura 7.33: Módulo Incepetion da rede GoogLenet - A parte intermediária da rede GoogLenet é formada por uma sequência de módulos Inceptions separados por camadas pooling (Figura 7.32). Cada módulo apresenta quatro caminhos para o mesmo dado de entrada, e na saída, os resultados são concatenados [39, p. 274].

A partir da entrada do módulo inception, as cópias do elemento de entrada seguem ao mesmo tempo por quatro caminhos. Ao final destes caminhos não se altera o tamanho da imagem, porém o número de canais é alterado de formas diferentes, sendo a escolha do número de canais de cada camada um hiperparâmetro. Na saída do módulo ocorre uma concatenação de todos estes canais, formando um único elemento de mesma dimensão que na entrada e com número de canais que é soma de todos que resultaram de cada caminho.

O primeiro caminho tem apenas uma convolução \(1\text{ x }1\), conhecida como bottleneck, que tem como principal função preservar as dimensões (altura e largura) mas diminuir o número de canais, o que reduz o custo computacional e o número de parâmetros [38, p. 220]. Como esta convolução inclui mais não linearidade com baixo custo, inclui-se também nas camadas de entrada uma convolução \(1\text{ x }1\), contribuindo para uma otimização na primeira parte da rede [35, p. 453]. Esta mesma camada foi acrescentada no início de cada um dos caminhos 2 e 3 para reduzir a complexidade do modelo. Após reduzir o número de camadas se inclui filtros maiores, possibilitando processar as informações em diferentes escalas, sendo que no segundo caminho os filtros são \(3\text{ x }3\) e no quarto caminho \(5\text{ x }5\) [39, p. 274].

Todos os caminhos, até mesmo o quarto que inclui uma camada de MaxPool, apresentam apropriados padding para manter a mesma dimensão dos canais que na entrada. Como o MaxPool não altera o número de canais, é incluído no final do quarto caminho uma convolução \(1\text{ x }1\), reduzindo o volume.

Ao concatenar no final todos os canais de cada caminho, o módulo inception segue a hipótese de que a informação visual pode ser processada em várias escalas e que os resultados agregados permitem ao próximo nível extrair várias características de diferentes escalas ao mesmo tempo [38, p. 222]. Na rede GoogLenet da Figura 7.32, vê-se três agrupamentos de módulos inception intercalados por Maxpooling \(3\text{ x }3\), totalizando 9 módulos.

O diagrama anterior da GoogLenet é uma das representações mais simplificadas do modelo, pois como é visto na Figura 7.34, a arquitetura original inclui dois classificadores que correm paralelamente com os outros blocos descritos anteriormente, um que se inicia depois do terceiro módulo inception e o outro depois do sexto módulo [35, p. 456]. Cada classificador funciona parecido com a parte final da rede, em que ocorre a classificação [40]. Os classificadores são formados por uma camada AvgPooling, seguida por uma de convolução, duas camadas totalmente conectadas e na saída uma função de ativação Softmax.

Existe uma peculiaridade ao treinar as redes mais profundas, pois, na retropropagação dos erros, as taxas reduzem a valores muito próximo de zeros, dificultando a convergência do algoritmo. A técnica adotada pelo GoogLenet para garantir a convergência foi incluir o cálculo do gradiente dos erros destas classificações intermediárias na retropropagação do erro [35, p. 456].

Figura 7.34: Arquitetura da rede GoogLenet com classificadores intermediários - A rede GoogLenet com dois classificadores, um no terceiro módulo inception e o outro no sexto módulo. Estes classificadores intermediários reduzem o efeito de desaparecimento dos gradiente do erro [44].

7.2.3.5 ResNet

A Rede Neural Residual (ResNet) venceu a competição ImageNet em 2015 com uma taxa de erro de \(3.6\%\). A rede desenvolvida por um grupo de pesquisa da Microsoft inclui várias técnicas de otimização e regularização dos modelos anteriores, principalmente da GoogLenet. Enquanto o ponto característico da rede GoogLenet são os módulos inceptions, na ResNet as unidades residuais permitiram treinar redes ainda mais profundas. Entre os principais modelos da ResNet são encontradas redes com 50, 101, 152 camadas de pesos [38, p. 230], mais que o dobro do número da GoogLenet com 22 camadas.

Da mesma forma que a GoogLenet, a rede ResNet pode ser divida em três partes, sendo que a primeira e a última parte seguem a arquitetura da GoogLenet, e as camadas intermediárias incluem as unidades residuais. As camadas de entrada que permitem uma redução considerável da dimensão da imagem incluem uma camada de convolução com 64 canais e filtros \(7\text{ x }7\) de \(\text{stride}=2\), seguida por uma camada \(3\text{ x }3\) de MaxPooling com \(\text{stride}=2\). A última parte da rede, a estrutura de classificação, apresenta as mesmas camadas da GoogLenet, a camada Global de Pooling média de dimensão 1024 e apenas uma camada totalmente conectada com 1000 unidades representando as classes. Lembrando que a substituição do processo de flattering pela média global permitiu reduzir a proporção de parâmetros nas últimas camadas.

Figura 7.35: Arquitetura da rede ResNet - A estrutura geral da rede ResNet também pode ser dividida em três partes. Semelhante a GoogLenet, contém uma camada convolucional e pooling para reduzir as dimensões da imagem. Uma parte com os módulos de unidades residuais, e no final uma camada de pooling global e uma Full Conect para classificação [35, p. 458].

Como descrito no Tópico rede GoogLenet ao acrescentar mais camadas, o número de parâmetros pode aumentar de forma que dificulte o treinamento, não só pelas limitações de recursos computacionais, mas também pela possibilidade de overfitting e demora de convergência do algoritmo. O modelo GoogLenet adotou várias abordagens de otimização e regularização, incluindo camadas de classificação intermediária para garantir que o modelo pudesse convergir, evitando o efeito de desaparecimento dos pesos (vanishing gradients), que em certos momentos tendiam a zero [35, p. 456].

Uma das técnicas do ResNet que colaboraram para acelerar a convergência no treinamento foi a normalização em batch. Este método se tornou referência para vários modelos de CNN, pois até aquela época cada modelo adotava abordagens diferentes no treinamento, como as classes intermediárias do GoogLenet [40]. A normalização é aplicada individualmente por camada, sendo que a normalização dos dados ocorre com base nas estatísticas dos agrupamentos minibatch adotados no treinamento, que foram vistos rapidamente em MLP [39, p. 280]. Nas redes ResNet a normalização é aplicada nos dados no momento de transição entre a camada de convolução e a de ativação.

Mesmo conseguindo convergir redes mais profundas, identificou-se nos modelos que ocorria uma degradação da acurácia ao se acrescentar mais camadas [45]. Antigamente se tinha a intuição de que ao se partir de um modelo com número reduzido de camadas para uma rede mais profunda, o erro não deveria aumentar, pois no mínimo a rede mais profunda teria uma parte das suas camadas copiadas da outra rede e a outra parte funcionaria como funções de identidade. Com mais camadas, a otimização de um modelo se torna mais complexa mesmo para problemas facilmente mapeados em redes menores [45]. A ideia na ResNet para lidar com esta complexidade foi forçar que as camadas realizassem o mapeamento da saída incluindo como referência a própria entrada, ou seja, um mapeamento residual [35, p. 457].

No mapeamento comum das camadas na Figura 7.36 se imagina que a partir de uma entrada \(x\) se busca com o treinamento estabelecer uma resposta esperada \(h(x)\). No caso do mapeamento residual se inclui um desvio do dado de entrada (\(x\)) na saída para forçar um modelo \(h(x) - x\). Com isso se espera que seja mais fácil otimizar um modelo com referência, o mapeamento residual, e que este consiga rapidamente se ajustar a funções identidade, garantindo que as camadas no mínimo estabeleçam a performance das camadas anteriores [39, p. 288]. Os desvios, conexões residuais, também minimizam os efeitos de desaparecimento dos pesos, pois permitem um fluxo alternativo dos gradientes, contribuindo para a retropropagação do erro [38, p. 231].

Figura 7.36: Mapeamento convencional e o residual da rede ResNet - a - Mapeamento tradicional da entrada e saída das camadas; b - Mapeamento em uma unidade residual da rede ResNet. No mapeamento comum, para uma entrada \(x\) se busca estabelecer uma resposta esperada \(h(x)\). No modelo residual se inclui um desvio da entrada (\(x\)) na saída para forçar uma resposta \(h(x) - x\) [35, p. 457]

A conexão residual parte da entrada de uma unidade residual em direção a saída da mesma, somando a informação de entrada com a resposta antes da camada de ativação ReLu (Figura 7.37). Cada unidade residual tem duas camadas de convolução \(3\text{ x }3\), com \(\text{stride}=1\) e configuração de padding para manter as dimensões. Entre as duas camadas existe uma camada de normalização antecedendo uma ativação ReLu.

Figura 7.37: Unidade residual da rede ResNet - Na parte intermediária da rede ResNet existe uma sequência de módulos com unidades residuais. Cada unidade residual tem duas camadas de convolução intercaladas por uma ativação ReLu e uma normalização que também é aplicada na saída das convoluções [35, p. 457].

Após uma sequência de unidades residuais de mesma configuração, entre os módulos, é dobrado o número de canais e ao mesmo tempo se reduz pela metade a largura e altura dos canais. Entre as unidades residuais não são utilizadas camadas pooling, assim, para reduzir as dimensões dos canais é utilizado \(\text{stride}=2\) na convolução que encerra um módulo. Desta forma, na última unidade residual dos módulos, a entrada tem dimensão diferente da saída. Para poder somar os valores é necessário corrigir as dimensões da entrada com uma convolução \(1\text{ x }1\) de \(\text{stride}=2\) e de mesmo número de canais da saída da unidade [39, p. 289].

A estrutura dos módulos com as unidades residuais lembram os blocos da rede VGG, em que cada bloco apresenta uma sequência de camadas de convolução com as mesmas dimensões, e sempre filtro \(3\text{ x }3\). De um bloco para o outro no VGG, o número de canais também dobra e a altura e a largura são reduzidas pela metade, neste caso pelo efeito do MaxPooling. O ResNet apresenta 4 módulos, em que o número de unidades residuais varia de modelo a modelo como indicado na Figura 7.38. O ResNet-34, por exemplo, com 34 camadas de pesos contém respectivamente nos quatro módulos, três unidades residuais com saída de 64 canais, quatro unidades com 128 canais, seis unidades com 256 canais e três unidades com 512 canais [45].

Figura 7.38: Arquitetura padrão da ResNet - Existem várias versões da ResNet, sendo que a parte inicial e a final das redes são semelhantes, e o que geralmente muda é quantidade de unidades residuais em cada um dos quatro módulos, na parte intermediária da rede [35, p. 457].

7.2.4 Aprendizado por transferência

Treinar uma rede neural do zero é uma tarefa complicada, pois necessita de uma enorme quantidade de dados e poder computacional [38, p. 242]. Em muitos casos podemos não ter uma quantidade suficiente de algum dos dois, mas isso não impede que criemos nossos modelos. Para isso contamos com uma técnica conhecida como aprendizagem por transferência, que consiste basicamente em utilizar-se modelos já treinados na resolução de nossos problemas. Nesse caso assumimos que muitos dos fatores que explicam o contexto \(P_1\) (situação na qual o modelo foi treinado) também podem explicar nossa novo contexto \(P_2\) [23, p. 536].

Conseguimos utilizar essa técnica pois mesmo modelos treinados em escopos diferentes acabam aprendendo a detectar características parecidas nas camadas mais iniciais, com maior especificação nas camadas mais profundas. Podemos ver isso na Figura 7.39, onde temos a representação de quatro redes diferentes sendo a primeira voltada a trabalhar com imagem de pessoas, a segunda com carros, a terceira com elefantes e a última com cadeiras. Mesmo esses sendo objetos completamente diferentes, as redes aprendem, nas camadas iniciais a detectar bordas e quinas, que são características compartilhadas por todos os itens.

Figura 7.39: Diferentes CNN’s e seus mapas de características em diferentes camadas - Na primeira coluna temos as características aprendidas por uma rede especializada no trabalho com rostos humanos, na segunda coluna com carros, na terceira com elefantes e na quarta com cadeiras [38, p. 253].

Existem três principais maneiras de se realizar a transferência de aprendizado [38, p. 254], sendo que cada uma delas se enquadra melhor em um cenário ou em outro, são elas:

• Usar uma rede pré-treinada como classificador
• Usar uma rede pré-treinada como um extrator de características
• Usar uma rede pré treinada para ajuste fino

O método de usar uma rede pré-treinada como classificador é melhor quando nosso problema tem um domínio muito parecido com a rede já treinada que iremos utilizar, sendo que temos apenas que a encaixar em nosso uso, não sendo necessário treinamento adicional.

O método usar uma rede pré-treinada como um extrator de características é útil quando estamos resolvendo um problema que tem várias características comuns com uma rede pré treinada mas não de maneira que possamos utilizar como na aproximação anterior. O que fazemos então é “congelar” as camadas da rede que extraem características (ou seja, as camadas de convolução) e substituir a rede totalmente conectada do final, colocando em seu lugar outra rede que classifique conforme nossa necessidade e realizamos seu treinamento.

Figura 7.40: Rede VGG-16 - Temos, de cima para baixo, as camadas “congeladas”, as camadas que serão removidas e a camada que será adicionada e treinada [38, p. 257].

Na Figura 7.40, temos um exemplo do livro de Mohamed Elgendy [38], onde se queria realizar a classificação de cachorros e gatos. A Rede VGG-16 foi escolhida pois foi treinada na base de dados ImageNet, que contém muitos exemplos de cachorros e gatos, com isso ela poderia se adaptar bem ao nosso problema.

Os dois métodos anteriores são usados quando temos um domínio parecido, já este, o terceiro método, que usa a rede pré-treinada para ajuste fino, enquadra-se em problemas que têm propriedades bem diferentes. Mesmo nestes casos conseguimos utilizar redes pré-treinadas, pelos motivos já ditos anteriormente, que as redes, principalmente em suas camadas iniciais, aprendem a detectar características parecidas, ficando mais específicas conforme sua profundidade [38, p. 259].

No método que usa a rede pré-treinada para ajuste fino, temos algumas possibilidades. Uma delas é “congelar” as primeiras camadas convolucionais e retreinar o resto da rede, o que estaremos fazendo então é um ajuste fino (também conhecido como fine-tune) nas camadas mais profundas da rede, para que consigam se adaptar ao nosso problema atual. E a outra é a de não “congelar” nenhuma camada e retreinar a rede toda, neste caso, mesmo tendo que gastar um tempo maior e ser necessário uma maior quantidade de dados, a rede tende a convergir mais rapidamente a uma solução ótima, em comparação a uma iniciação randômica [38, p. 259].

No livro “Deep Learning for Vision Systems” de Mohamed Elgendy, são apresentadas algumas dicas de como escolher a melhor técnica de transferência de aprendizado para alguns tipos de cenários, sendo elas apresentadas na Tabela 7.3:

Tabela 7.3: Diferentes cenários onde podemos utilizar a transferência de aprendizado [38, p. 262].

Cenário	Quantidade de dados disponíveis	Similaridade entre a rede pré-treinada e a nova base de dados	Método
1	Pequena	Similar	Usar uma rede pré treinada como classificador
2	Grande	Similar	Ajuste fino na rede totalmente conectada
3	Pequena	Muito diferente	Ajuste fino em uma parte da rede
4	Grande	Muito diferente	Ajuste fino em toda a rede

7.2.5 Redes neurais na prática

Ao estudar os diferentes modelos de CNN’s percebemos que o principal fator para melhorar a acurácia das redes foi o aumento no número de camadas, tornando as redes mais profundas. Destaca-se que a construção de modelos mais profundos só foi possível pela evolução da performance de hardware, principalmente memória e unidades de processamento, e desenvolvimento de softwares mais específicos, conhecidos como frameworks para Deep Learning [39, p. 36].

O treinamento das redes envolve milhares de operações com elementos multidimensionais, ou seja, arrays n-dimensionais com número arbitrário de eixos, conhecidos como tensores [39, p. 42]. Tensores com apenas uma dimensão correspondem matematicamente aos vetores, enquanto os de duas dimensões são as matrizes. No caso das redes CNN’s, muitas vezes as entradas são imagens coloridas que podem ser interpretadas como tensores de três dimensões: a altura, a largura e o volume da imagem (canais RGB). Dentro da rede ocorre uma série de multiplicações e somas a partir do tensor de entrada, resultando em diferentes tensores tridimensionais.

A realização de todas as operações só é possível devido às unidades de processamento das máquinas, que permitem a interação da unidade lógica aritmética (ALU) com a memória. Quando as primeiras redes foram desenvolvidas, o principal recurso de processamento eram as CPU’s, um processador de propósito geral em que a ALU realiza apenas um cálculo por vez. Como possui aplicações mais gerais precisa de acesso constante à memória para leitura de instruções e armazenamento de dados, o que é uma desvantagem em relação ao tempo de processamento, conhecida como “gargalo de von Neumann” [46]. Geralmente para tornar mais rápido o acesso a memória, são integradas tecnologias mais sofisticadas aos caches, porém de tamanho limitado devido ao custo [39, p. 260].

As limitações de armazenamento e processamento relacionados a uma única CPU inviabilizam o treinamento de redes mais profundas. O que permitiu a evolução das redes foi a adaptação de unidades de processamento com aplicações mais específicas. A maioria das redes modernas são implementadas com base em unidades de processamento gráfico (GPU’s). Originalmente estes componentes foram desenvolvidos para aplicações gráficas, principalmente para renderização dos video games [23, p. 439]. Entretanto, grande parte da abordagem de processamento da GPU também se mostrou compatível com os cálculos necessários para treinar as redes neurais.

A GPU consegue maior capacidade de processamento do que uma CPU, pois integra várias ALU’s em um único processador, o que permite a realização de milhares de operações simultaneamente [46]. Esta estratégia é ideal para aplicações que se adequam ao processamento paralelo, como multiplicação de matrizes de uma rede neural, que envolvem operações independentes [23, p. 440]. As GPU’s foram construídas para realizar operações mais simples, sem envolver muitas ramificações como geralmente é necessário no fluxo de trabalho da CPU. A maior parte dos cálculos do treinamento das redes são previsíveis, com algoritmos que não necessitam de controles sofisticados [23, p. 440].

Se por um lado as operações das redes não exigem grande complexidade computacional, por outro, demandam grande quantidade de memória. Durante o treinamento é preciso armazenar os parâmetros, os valores de ativação, e os gradientes, ou seja, uma quantidade de dados além do limite da cache associada à CPU [23, p. 440]. Neste sentido, além de permitir processamento paralelo, diminuindo o tempo de treinamento, a GPU também oferece maior quantidade de memória.

A utilização da GPU para o treinamento das redes se tornou ainda mais comum após a adaptação para propósitos mais gerais. Um dos principais modelos de GPU, da NVIDIA, suporta uma programação CUDA para o desenvolvimento de códigos arbitrários semelhantes à linguagem C [23, p. 440]. Assim, a GPU pode executar diferentes rotinas que não estejam só associadas a subrotinas de renderização.

Para garantir códigos de GPU de alta performance, foram construídos ao longo dos anos diferentes bibliotecas que lidam com computação numérica, principalmente envolvendo convoluções e outras operações com tensores [23, p. 441]. Assim, no desenvolvimento das redes não é necessário saber a programação a nível de CUDA, que é mais complexa e envolve computação paralela e distribuída. Geralmente estas bibliotecas, ou frameworks, têm suporte tanto em GPU quanto CPU. As primeiras gerações de muitos frameworks foram desenvolvidas por meio de parcerias entre Universidades e grandes empresas com interesse em Deep Learning. Algumas das bibliotecas mais comuns, destacadas na Figura 7.41, são o PyTorch e Caffe2 mantidos pelo Facebook, o TensorFlow pela Google, o MXNet pela Amazon e o CNTK pela Microsoft [40].

Figura 7.41: Principais frameworks para Deep Learning - Para facilitar a manipulação de tensores e a utilização de GPU’s foram desenvolvidos diferentes frameworks. A maior parte das primeiras gerações dos frameworks surgiram como parcerias entre universidades e grandes empresa [40].

Mesmo com o aumento do desempenho da GPU em relação a CPU para treinar as redes, em muitos casos, uma única máquina não é suficiente para todo o processamento. Com a possibilidade do paralelismo se tornou comum distribuir a carga de trabalho entre várias máquinas. No entanto, montar uma rede própria de GPU é um investimento alto, e a tecnologia também iria depreciar em poucos anos, pois os modelos de GPU estão evoluindo rapidamente para acompanhar as redes cada vez maiores [47]. Uma alternativa para as redes locais é utilizar servidores de GPU em nuvem oferecidos por provedores como Amazon, Google, Microsoft entre outros.

Nos últimos anos aumentou a oferta de serviços na nuvem para treinar CNN’s, sendo que os custos são com base no tipo de tecnologia da GPU disponível, no tempo de processamento e na quantidade de armazenamento [47]. Alguns provedores oferecem alguns serviços gratuitos. As redes podem ser desenvolvidas, diretamente, em plataformas oferecidas pelos próprios provedores, que, geralmente, apresentam uma IDE baseada em Jupyter Notebooks. Cada plataforma apresenta facilidades para determinados frameworks, geralmente para aquelas bibliotecas que também prestam suporte [47]. O GoogleCloud, por exemplo, apresenta várias ferramentas para integrar com o TensorFlow.

O GoogleCloud oferece além dos serviços de GPU a alternativa de acesso às TPU’s como recursos de computação em nuvem. A TPU (unidades de processamento de tensor) foi projetada especificamente para trabalhar com redes neurais e funciona como processador de matriz especializado. Como a sequência de cálculos já é previamente conhecida, foram conectados vários multiplicadores e somadores, formando uma matriz de operadores, denominada matriz sistólica [46]. Uma vantagem da TPU em relação a CPU e a GPU é a redução do gargalo de von Neumann, pois os dados são todos carregados de uma única vez da memória, não precisando o acesso durante os cálculos [46].

No tópico sobre backpropagation foi apresentado um exemplo de aplicação de rede MLP para reconhecimento de dígitos em que implementamos na linguagem Python. No código foi desenvolvido manualmente a estrutura da rede, as etapas do treinamento e as funções, utilizando principalmente bibliotecas que lidam com cálculos em Arrays Multidimensionais, como o Numpy. No exemplo MLP, ao manipular os dados como array do numpy não surgiram inconsistências e também não nos deparamos com operações muito complexas, pois até aquele momento as aplicações não envolviam redes muito densas, que exigissem várias otimizações e regularizações. Em modelos de redes maiores, a utilização do algoritmo backpropagation é um desafio maior e muitas vezes pode ser difícil garantir a convergência apenas utilizando as bibliotecas tradicionais de computação numérica [36, p. 153].

Por outro lado, os frameworks que acabamos de apresentar, como o TensorFlow e o Pythorch, foram construídos especificamente para lidar com Deep Learning, podendo, por exemplo, disponibilizar automaticamente várias funções de otimização e regularização. Os frameworks de Deep Learning geralmente apresentam uma estrutura de dados multidimensionais, tratadas como uma classe tensor, que substitui o “ndarray” do numpy [39, p. 44]. Esta estrutura de dados de tensor apresenta algumas vantagens em relação ao tradicional array do numpy que se adequam melhor a manipulação de dados nas redes. O primeiro ponto é que o numpy apresenta por default uma precisão de \(64 \text{ bits}\), enquanto os tensores geralmente usam \(32 \text{ bits}\). Como a precisão de \(32 \text{ bits}\) é suficiente para trabalhar com as redes, ao se reduzir o tamanho dos dados, ocupa-se menos memória e torna as operações mais rápidas [35, p. 474].

Por padrão a manipulação das variáveis são direcionadas para os cálculos na CPU, entretanto, quando existe disponível diferentes dispositivos de CPU e GPU pode ser interessante distribuir os cálculos e armazenamento [39, p. 219]. Diferente do Numpy, os frameworks de Deep Learning possuem suporte para lidar com vários dispositivos ao mesmo tempo [39, p. 44]. Anteriormente destacamos que o propósito da utilização das GPU’s nas redes é acelerar o treinamento, principalmente adotando processamento distribuído e paralelo, porém, se a manipulação dos dados não for adequada, ocorrerá muitas transferências entre dispositivos, assim, o tempo de processamento pode aumentar [39, p. 222]. Geralmente, ao se utilizar os frameworks configurados com as GPU’s e CPU’s, não é necessário se preocupar na forma como ocorrem estas transferências, pois os processamentos são otimizados com base em gráficos computacionais [35, p. 368].

O que tem popularizado ainda mais as CNN’s mesmo fora dos meios acadêmicos é o desenvolvimento de interfaces de programação que tornam mais simples a construção e o treinamento das redes neurais. Keras, um dos mais conhecidos API para Deep Learning em alto nível, foi desenvolvido por François Chollet como um projeto de pesquisa, que foi disponibilizado como software livre em 2015 [35, p. 292]. Foi escrito em Python e funciona como um mecanismo de computação subjacente que roda sob diferentes frameworks de backend, alguns identificados na Figura 7.42, os quais oferecem o suporte de computação numérica, como TensorFlow, Theano, CNTK e MxNet [35, p. 292].

Grande parte do trabalho com as redes neurais pode ser implementado direto com o API de alto nível, incluindo o desenho da arquitetura, as funções, algoritmo de treinamento, otimizadores e módulos de regularização. Para implementações que necessitam de maiores customizações é necessário recorrer aos frameworks de mais baixo nível, como o TensorFlow. O TensorFlow, criado por um grupo de pesquisa da Google e liberado como software livre em 2015, tem a sua própria implementação de keras, o tf.keras [35, p. 368].

O API tf.keras tem como backend apenas o TensorFlow (Figura 7.42), porém apresenta maiores facilidades para integrar com customizações do backend. A inclusão de novos códigos pode ser feita a partir da linguagem Python e automaticamente o API converte para funções do tipo TensorFlow que possuem base no C++ [35, p. 398]. Muitas vezes essas adaptações ocorrem quando se precisa de um controle maior, ou customizar funções, camadas, módulos de regularização, processos de inicialização, ou medidas de avaliação [35, p. 398].

Figura 7.42: Implementações do API Keras - a - Implementação geral do API keras-team que é compatível com diferentes backends, como TensorFlow, Theano, CNTK e MxNet. b - O API tf.keras tem como backend apenas o TensorFlow e comporta aplicações específicas deste framework [35, p. 292]

No momento a última versão estável do TensorFlow é a 2.4, sendo que a primeira versão do TensorFlow 2.0 foi lançada em março de 2019 [48]. Enquanto que nas versões 1.0, o módulo simbólico é a parte central [35, p. 396], principalmente pela preferência da abordagem por gráficos estáticos, a partir das versões 2.0 se começou a ter uma programação mais imperativa de forma semelhante ao PyTorch, e que apresenta como default gráficos dinâmicos [39, p. 516]. O módulo estático busca maior otimização do código, sendo que após a definição de todo o processo e construção do gráfico não se tem mais a dependência do código [40]. No formato dinâmico a construção e a execução dos gráficos não podem ser desvinculadas, pois ocorrem simultaneamente. Geralmente, os gráficos dinâmicos são mais fáceis de debugar e apresentam menores inconsistências [40].

7.3 Redes Neurais Siamesas

O primeiro trabalho com redes neurais siamesas em 1994 tinha a proposta de comparar duas assinaturas manuscritas, verificando se as duas eram originais ou se uma delas era falsa [49, p. 75]. Grande parte das redes neurais para classificação com imagens utiliza a estratégia de apresentar o objeto para identificar o que é, enquadrando nas classes definidas no treinamento. As redes siamesas apresentam o problema de uma forma diferente, em vez de descobrir o que foi apresentado, a ideia é comparar duas entradas, verificando se fazem parte da mesma classe ou não.

Após a utilização das redes siamesas para reconhecimento de assinaturas surgiram diferentes aplicações para análise de imagens com objetivo de avaliar a similaridade entre elas. Na área da saúde, as redes siamesas já foram testadas por diferentes trabalhos para detecção de doenças a partir da análise de imagens de exames [49, p. 81]. Já foram apresentados trabalhos na área da farmácia para comparação de composições químicas, e na biologia, para avaliar sequências de DNA e classificar cromossomos [49, p. 78]. Existem adaptações destas redes em diferentes setores, como na robótica, no desenvolvimento de software e no sensoriamento remoto [49, p. 82].

Uma das aplicações que mais teve repercussão foi na verificação de faces, como no trabalho de Chopra et al. (2005) [50]. Taigman et al. (2014) apresentaram uma rede para verificação de faces a partir de fotos, como um projeto do Facebook [51]. Sabri e Kurita (2018) trabalharam com reconhecimento de faces e expressões faciais [52]. As redes neurais siamesas também ganharam popularidade no reconhecimento de imagem one-shot, em particular pelo estudo de Koch et al. (2021) [49, p. 81].

Diferente dos modelos tradicionais de redes para classificação que precisam de uma grande quantidade de entradas de treinamento para cada classe, nas redes siamesas one-shot, geralmente é necessário apenas um exemplo para cada classe [53]. O propósito da rede não é reconhecer a entrada a partir de diferentes classes, o que exige muitos dados de treinamento, e sim, comparar a similaridade entre duas imagens. Por exemplo, em um reconhecimento facial dos funcionários de uma empresa, em vez de treinar uma rede com várias fotos de cada pessoa para que aprenda a classificar um por um, pode ser interessante utilizar uma siamesa one-shot que compara uma entrada com as referências verificando se corresponde a algum funcionário.

Considerando que os vídeos podem ser tratados como uma sequência de imagens, muitas das técnicas de processamento de imagens com redes siamesas foram bem adaptadas para aplicações com vídeos. Além de aspectos estáticos presentes nas imagens, os vídeos podem oferecer informações de movimento e do estado de objetos em diferentes contextos e momentos [49, p. 83]. Por exemplo, com vídeos é possível não só reconhecer um objeto em uma imagem isolada, como também rastreá-lo ao longo dos quadros de gravações [54]. Estas redes conseguiram reconhecer pessoas até mesmo com base no estilo de caminhada, como mostrou um estudo com imagens de vídeos de segurança [55].

O uso das redes com dados de vídeos tem mostrado várias oportunidades na área de segurança, além do monitoramento de pessoas também existem linhas de pesquisa para o setor de veículos e trânsito. O sistema PROVID produzido por Liu et al. (2017) é um exemplo do uso das redes siamesas para identificação de veículos com base nas placas [56]. Os estudos de redes siamesas para detecção dos limites das estradas e de contornos em vídeos na perspetiva da direção de veículos pode ajudar o desenvolvimento de automóveis autônomos [57].

As possibilidades das redes siamesas se estendem além do processamento de imagens e da visão computacional, já foram apresentados estudos para análise de áudios e no processamento de linguagem natural. Um exemplo de aplicação com áudio foi a rede siamesa de Zhang et al. (2018), desenvolvida para avaliar a similaridade entre sons originais e imitações de vozes para poder diferenciá-las [54]. A área de processamento de linguagem natural se propõe gerar e compreender automaticamente a linguagem humana a partir de dados de comunicação, como em documentos com textos e mensagens. Por exemplo, na proposta de González et al. (2019), as redes siamesas extraem as informações mais importantes de um texto para poder resumi-lo [58]. No trabalho de Das et al. (2016) foram avaliados questões de diferentes websites de perguntas e respostas, como Yahoo Answers e Stack Overflow, para poder detectar as semelhanças entre as mensagens [59].

7.3.1 Arquitetura

Como dito no tópico anterior de Redes Neurais Siamesas, o objetivo de se utilizar uma rede com arquitetura siamesa era comparar diferentes entradas e ter como resultado um valor que representasse sua semelhança ou diferença. O nome “siamesa” por si só já nos dá uma boa ideia de como será sua arquitetura, que consiste basicamente na utilização de duas redes idênticas, como na Figura 7.43, onde temos a rede proposta por Bromley et al. (1993) em seu artigo sobre verificação de assinaturas [60]. Nessa arquitetura temos uma camada de entrada de \(200 \text{ x } 8\) unidades e como saída um bloco de dados de \(16 \text{ x } 19\) unidades, o método utilizado para realizar a comparação entre os vetores de saída das duas redes foi calcular o cosseno do ângulo entre eles.

Figura 7.43: Arquitetura utilizada por Bromley et al. (1993) com duas redes recebendo os dados sobre assinaturas após seu pré-processamento. A rede contém uma camada de entrada com \(200 \text{ x } 8\) unidades e uma saída de \(16 \text{ x } 19\) unidades. [60].

Na Figura 7.44 temos um exemplo de outra arquitetura, nesse caso a apresentada por Chopra et al. (2005). Um aspecto importante que devemos notar é que tanto essa rede quanto a anterior tem os mesmo pesos em ambas as suas redes internas. Nesse caso se optou por utilizar a distância euclidiana entre os dois vetores de características resultantes das duas subredes.

Figura 7.44: Arquitetura utilizada por Chopra et al. [50]. Essa arquitetura de rede siamesa tem os parâmetros da rede compartilhados entre as duas. \(X_1\) e \(X_2\) são as duas entradas da rede e \(E_w\) é a saída da diferença euclidiana entre as saídas das duas redes (\(||G_w(X_1)-G_w(X_2)||\)).

Das redes neurais que apresentamos para aplicações no processamento de imagens e visão computacional, como MLP, CNN’s e siamesas, as abordagens de desenvolvimento, treinamento e operação seguem um padrão semelhante ao se pôr em prática. A utilização de frameworks tem facilitado as aplicações em redes neurais, disponibilizando comandos para criar camadas, montagem da arquitetura, funções de regularização e otimização, medidas de avaliação, algoritmos de treinamento, sendo que a maior parte dos recursos é facilmente adaptável para diferentes modelos de redes. Geralmente, a maior parte do trabalho de quem desenvolve essas redes está na obtenção e preparo dos dados de entrada.

Dependendo do tipo da rede, a imagem de entrada deve ser disponibilizada como um vetor, como na MLP, ou como um tensor, como na CNN’s, e no caso das siamesas pode ser que a entrada seja duas ou mais imagens ao mesmo tempo. Na maioria das vezes será necessário, dimensionar as imagens, estabelecer as classes, alterar o formato dos dados, e dividir as amostras de treinamento, teste e validação. Cada aplicação pode exigir uma abordagem diferente para que a rede aprenda o problema, o que muitas vezes exige que os dados sejam pré-configurados e organizados de forma que se adequem ao tipo de algoritmo adotado no treinamento.

Nas redes estudadas, utiliza-se o método supervisionado, especificamente o backpropagation, ou seja, durante o treinamento devem ser apresentados tanto as entradas do problema como as respostas correspondentes que são previamente conhecidas. Desta forma, o modelo consegue corrigir os parâmetros da rede considerando as diferenças entre as saídas e as respostas esperadas. No algoritmo de backpropagation, esta diferença é tratada por uma função de erro que o treinamento busca minimizar. No tópico backpropagation foi descrita uma das funções de erro que foram utilizadas pelos primeiros modelos de redes neurais, o erro quadrático (MSE). Com o aprimoramento das redes, a substituição por outras funções erros demonstrou melhores resultados no treinamento, como a entropia cruzada ou Cross-Entropy [33].

Dado a expressão da função custo entropia cruzada e de sua derivada:

\[ C = -\frac{1}{n} \sum_{x}[y \ln a + (1 - y) \ln(1 - a)] \tag{7.22} \]

\[ \frac{\partial C}{\partial w_j} = \frac{1}{n} \sum_{x} x_j (\sigma(z) - y) \tag{7.23} \]

se consegue avaliar que a derivada aumenta com o tamanho do erro (\(\sigma(z) - y\)). Considerando este comportamento e que o algoritmo de treinamento fica mais rápido quanto maior for a derivada da função custo, o método da entropia cruzada tende a demonstrar menores problemas com a desaceleração do aprendizado se comparado ao erro quadrático [33]. No erro quadrático, como a derivada da função custo depende diretamente da derivada da função de ativação, o treinamento poderá ficar estagnado nos pontos em que a ativação for próximo dos limites, particularmente se as funções de ativações forem sigmóides [33].

Geralmente, as funções erro quadrático e entropia cruzada são aplicadas em modelos que se pretende que a saída corresponda a um vetor de probabilidades em relação às classes. Desta forma, é possível associar cada valor a uma classe, ou seja, dado a entrada se determina qual a saída mais provável dentro dos exemplos estabelecidos no treinamento. Outras funções de custo mais comuns nas redes siamesas são as por técnica de ranqueamento, como a perda contrastiva e as funções triplets. No ranqueamento, a saída da rede é estabelecida pelas distâncias entre os dados de entrada de acordo com uma distribuição dos exemplos apresentados no treinamento [61]. Neste caso, as entradas que pertencem a uma mesma classe tendem a ficar mais próximas, ganhando uma posição de maior prioridade que elementos com menor semelhança, os quais vão se afastando.

O primeiro modelo de rede siamesa, que comparava as assinaturas [60], utilizou a função erro contrastiva [62]:

\[ L(W, Y, X_1, X_2) = (1 - Y)\frac{1}{2}(E_w)^2 + (Y) \frac{1}{2} {max(0,m - E_w)}^2 \tag{7.24} \]

em que são apresentadas pelo menos duas entradas na rede com propósito de comparar (ou contrastar) e determinar a similaridade. Quando o par de entrada é semelhante (\(X_1, X_2\)) o parâmetro \(Y\) recebe valor \(0\), e quando são de classes diferentes (\(X_1, X’_2\)), \(Y = 1\). Os pesos da rede (\(W\)) são corrigidos de forma que a distância (\(E_w\)) entre dados semelhantes fique menor e os mais diferentes se afastem [62]. Para isto é estabelecido uma margem (\(m\)) de ajuste, a qual garante uma distância mínima separando o que pertence ou não a um mesmo grupo, \(E_W (X_1, X_2) + m < E_W (X_1, X’_ 2 )\).

A função de erro Triplet tem demonstrado bons desempenhos em alguns estudos com redes siamesas. Diferente da função contrastiva, na rede Triplet se utiliza três dados como entrada no treinamento, ou seja, uma siamesa com três sub-redes idênticas em vez de duas. Neste método, compara-se ao mesmo tempo o valor âncora (\(x^a\)), ou valor de referência, com um padrão semelhante (caso positivo \(x^p\)), e com um padrão diferente (caso negativo \(x^n\)) de acordo com a função erro [63]:

\[ C = \sum_{i}\left[||f(x_i^a) - f(x_i^p)||_2^2 - ||f(x_i^a) - f(x_i^n)||_2^2 + \alpha\right] \tag{7.25} \]

Considerando que as funções \(f(x) \in R\) podem ser interpretadas como a aplicação de cada sub-rede, o algoritmo de treinamento deve buscar ordenar as entradas com base na similaridade relativa. Assim, a distância entre a âncora e o padrão positivo deve ser menor do que em relação ao caso negativo, como demonstrado na Figura 7.45. [63]. Da mesma forma que no método contrastivo é aplicada uma margem (\(\alpha\)) de ajuste.

Figura 7.45: Comportamento da função erro Triplet. A função Triplet reduz a distância entre os exemplos similares, ou seja, entre a âncora e o padrão positivo, e aumenta a distância entre o padrão diferente (caso negativo) e a âncora [63].

Refêrencias

[23] I. Goodfellow, Y. Bengio, e A. Courville, Deep Learning. MIT Press, 2016.

[24] A. Chiang, “IBM Deep Blue at Computer History Museum”. 2020, [Online]. Disponível em: https://commons.wikimedia.org/wiki/File:IBM_Deep_Blue_at_Computer_History_Museum_(9361685537).jpg.

[25] S. R. y Cajal, Comparative study of the sensory areas of the human cortex. Clark University, 1899.

[26] W. S. McCulloch e W. Pitts, “A logical calculus of the ideas immanent in nervous activity”, The bulletin of mathematical biophysics, vol. 5, nº 4, p. 115–133, 1943.

[27] Glosser.ca, “Artificial neural network with layer coloring”. 2013, [Online]. Disponível em: https://commons.wikimedia.org/wiki/File:Colored_neural_network.svg.

[28] S. Russell e P. Norvig, “Artificial intelligence: a modern approach”, 2016.

[29] H. Simon, Redes Neurais: Principios e pratica, 2º ed. São Paulo: Bookman, 1999.

[30] cs231, “Cartoon drawing of a biological neuron”. 2021, [Online]. Disponível em: https://cs231n.github.io/neural-networks-1/.

[31] T. Rateke, “Tecnicas Subsimbolicas: Redes Neurais”. LAPIX (Image Processing; Computer Graphics Lab) Universidade Federal de Santa Catarina, Florianopolis, [Online]. Disponível em: http://www.lapix.ufsc.br/ensino/reconhecimento-de-padroes/tecnicas-sub-simbolicas-redes-neurais/.

[32] A. de P. BRAGA, A. Carvalho, e T. B. Ludemir, “Fundamentos de redes neurais artificiais”, Rio de Janeiro: 11a Escola de Computação, 1998.

[33] M. A. Nielsen, Neural Networks and Deep Learning. Determination Press, 2015.

[34] J. A. Herts, A. S. Krogh, e R. G. Palmer, Introduction to the theory of neural computation. New York: CRC Press, 2018.

[35] A. Geron, Hands-on machine learning with Scikit-Learn, Keras, and TensorFlow: Concepts, tools, and techniques to build intelligent systems. O’Reilly Media, 2019.

[36] R. D. Adrian, “Deep Learning for Computer Vision with Python”. PyImageSearch, 2017.

[37] V. Dumoulin e F. Visin, “A guide to convolution arithmetic for deep learning”, arXiv preprint arXiv:1603.07285, 2016.

[38] M. Elgendy, Deep Learning for Vision Systems. Manning Publications, 2020.

[39] A. Zhang, Z. C. Lipton, M. Li, e A. J. Smola, Dive into Deep Learning. 2020.

[40] J. Johnson, “Deep Learning for Computer Vision - Fall 2019”. Website do curso EECS 498-007 / 598-005 na Universidade de Michigan, Michigan, Estados Unidos, 2019, [Online]. Disponível em: https://web.eecs.umich.edu/~justincj/teaching/eecs498/FA2020/.

[41] P. U. Stanford Vision Lab Stanford University, “ImageNet Large Scale Visual Recognition Challenge (ILSVRC)”. Website da competição ImageNet Large Scale Visual Recognition Challenge (ILSVRC), 2020, [Online]. Disponível em: https://image-net.org/challenges/LSVRC/.

[42] A. Krizhevsky, I. Sutskever, e G. E. Hinton, “Imagenet classification with deep convolutional neural networks”, Advances in neural information processing systems, vol. 25, p. 1097–1105, 2012.

[43] A. Canziani, A. Paszke, e E. Culurciello, “An analysis of deep neural network models for practical applications”, arXiv preprint arXiv:1605.07678, 2016.

[44] S. P. K. Karri, D. Chakraborty, e J. Chatterjee, “Transfer learning based classification of optical coherence tomography images with diabetic macular edema and dry age-related macular degeneration”, Biomed. Opt. Express, vol. 8, nº 2, p. 579–592, fev. 2017, doi: 10.1364/BOE.8.000579.

[45] K. He, X. Zhang, S. Ren, e J. Sun, “Deep residual learning for image recognition”, in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, p. 770–778.

[46] G. Developers, “Guia para iniciantes da Cloud TPU”. Website da Google Cloud, 2021, [Online]. Disponível em: https://cloud.google.com/tpu/docs/beginners-guide?hl=pt-br.

[47] A. von Wangenheim, “Deep Learning: Introdução ao Novo Coneccionismo”. LAPIX (Image Processing; Computer Graphics Lab) Universidade Federal de Santa Catarina, Florianopolis, 2018, [Online]. Disponível em: http://www.lapix.ufsc.br/ensino/reconhecimento-de-padroes/tecnicas-sub-simbolicas-redes-neurais/.

[48] G. Developers, “Versões da API TensorFlow”. Website do TensorFlow, 2020, [Online]. Disponível em: https://www.tensorflow.org/versions.

[49] J. M. Walker, Artificial Neural Networks, 3º ed. Nova Iorque, Estados Unidos: Humana/Springer Nature, 2021.

[50] S. Chopra, R. Hadsell, e Y. LeCun, “Learning a similarity metric discriminatively, with application to face verification”, in 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR05), 2005, vol. 1, p. 539–546.

[51] Y. Taigman, M. Yang, M. A. Ranzato, e L. Wolf, “Deepface: Closing the gap to human-level performance in face verification”, in Proceedings of the IEEE conference on computer vision and pattern recognition, 2014, p. 1701–1708.

[52] M. Sabri e T. Kurita, “Facial expression intensity estimation using Siamese and triplet networks”, Neurocomputing, vol. 313, p. 143–154, 2018.

[53] H. Lamba, “One Shot Learning with Siamese Networks using Keras”. Website Towards Data Science, Florian0polis, 2019, [Online]. Disponível em: https://towardsdatascience.com/one-shot-learning-with-siamese-networks-using-keras-17f34e75bb3d.

[54] H. Zhang, W. Ni, W. Yan, J. Wu, H. Bian, e D. Xiang, “Visual tracking using Siamese convolutional neural network with region proposal and domain specific updating”, Neurocomputing, vol. 275, p. 2645–2655, 2018.

[55] C. Zhang, W. Liu, H. Ma, e H. Fu, “Siamese neural network based gait recognition for human identification”, in 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2016, p. 2832–2836.

[56] X. Liu, W. Liu, T. Mei, e H. Ma, “Provid: Progressive and multimodal vehicle reidentification for large-scale urban surveillance”, IEEE Transactions on Multimedia, vol. 20, nº 3, p. 645–658, 2017.

[57] Q. Wang, J. Gao, e Y. Yuan, “Embedding structured contour and location prior in siamesed fully convolutional networks for road detection”, IEEE Transactions on Intelligent Transportation Systems, vol. 19, nº 1, p. 230–241, 2017.

[58] J.-A. Gonzalez, E. Segarra, F. Garcia-Granada, E. Sanchis, e L.-F. Hurtado, “Siamese hierarchical attention networks for extractive summarization”, Journal of Intelligent & Fuzzy Systems, vol. 36, nº 5, p. 4599–4607, 2019.

[59] A. Das, H. Yenala, M. Chinnakotla, e M. Shrivastava, “Together we stand: Siamese networks for similar question retrieval”, in Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), 2016, p. 378–387.

[60] J. Bromley, I. Guyon, Y. LeCun, E. Säckinger, e R. Shah, “Signature verification using a" siamese" time delay neural network”, Advances in neural information processing systems, vol. 6, p. 737–744, 1993.

[61] R. Gomez, “Understanding Ranking Loss, Contrastive Loss, Margin Loss, Triplet Loss, Hinge Loss and all those confusing names”. Blog Raul Gomez, 2019, [Online]. Disponível em: https://gombru.github.io/2019/04/03/ranking_loss/.

[62] R. Hadsell, S. Chopra, e Y. LeCun, “Dimensionality reduction by learning an invariant mapping”, in 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR06), 2006, vol. 2, p. 1735–1742.

[63] F. Schroff, D. Kalenichenko, e J. Philbin, “Facenet: A unified embedding for face recognition and clustering”, in Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, p. 815–823.