Capítulo 9 Espaço 3D

9.1 Geometria projetiva

Em alguns trabalhos realizados na visão computacional, a geometria euclidiana se torna insuficiente, pois as capturas de imagens com câmeras geram certos problemas, como linhas paralelas que se cruzam (como na Figura 9.1) e ângulos que não são preservados, fatos esses que ocorrem por estarmos projetando o mundo 3D em uma plano 2D [65, p. 321]. Nesses casos usamos outro tipo de geometria conhecida como geometria projetiva.

Figura 9.1: Linhas paralelas se cruzam - Como podemos ver nessa imagem de um trilho de trem, duas linhas que no mundo real são paralelas se cruzam no horizonte por causa da perspectiva [66].

Uma das vantagens de se utilizar a geometria projetiva é o fato que conseguimos representar transformação por simples multiplicação de matrizes, além de que as projeções nos provêem a noção de perspectiva, ou seja, objetos mais distantes têm um tamanho reduzido em relação a objetos mais próximos.

O espaço projetivo é definido por coordenadas homogêneas assim como o espaço Euclidiano é definido pelas coordenadas Cartesianas. Utilizamos esse espaço e sua geometria pois é a melhor maneira de se representar a relação entre uma imagem e o mundo físico, ou seja, a relação entre as coordenadas da câmera com as coordenadas do mundo real [19, p. 484].

9.1.1 Coordenadas homogêneas

As coordenadas homogêneas são a maneira como trabalhamos na geometria projetiva, elas diferem das coordenadas cartesianas por apresentarem uma componente a mais, ou seja, um ponto \((X, Y)^T \in \Re^2\) é representado, em coordenadas homogêneas, por \((X_1, X_2, X_3)^T\). A conversão entre os dois sistemas também é muito simples, um ponto \(X_c = (x, y)^T\) no sistema cartesiano é convertido a homogêneo da seguinte maneira:

\[ X_H = (wx, wy, w)^T \tag{9.1} \] e convertido ao cartesiano novamente por:

\[ x_c = \frac{wx}{w} \text{ e } y_c =\frac{wy}{w} \tag{9.2} \] Assim, quando \(w = 1\) nossas coordenadas são as mesmas do sistema cartesiano, como pode ser visto na Figura 9.2, onde \(w\) é representado por \(Z\). Os pontos que estão no formato \(X_H = (x, y, 0)^T\) são conhecidos como pontos ideais, e são os pontos onde as linhas se cruzam no infinito [67, p. 36].

Figura 9.2: Plano euclidiano e espaço projetivo - Nesta representação podemos ver um ponto do espaço euclidiano sendo projetado no espaço projetivo. [65, p. 605].

9.2 Homografia

As homografias (ou transformações perspectivas) são as transformações realizadas no espaço projetivo. Com elas podemos relacionar uma imagem de uma plano a outra imagem desse mesmo plano obtida de uma outra posição. Podemos observar uma representação disso na Figura 9.3, onde temos uma plano do objeto também o plano de duas imagens. O ponto \(\tilde{x_0}\) representa o ponto do plano do objeto na imagem 1 e o ponto \(\tilde{x_1}\) representa esse mesmo ponto na imagem 2 que é a vista do mesmo ponto a partir de outra posição. Relacionando esses dois pontos temos a homografia \(H_{10}\), que pode ser representada por:

\[ \tilde{x_0} = H_{10} \tilde{x_1} \tag{9.3} \] Onde \(x_0\) e \(x_1\) são vetores homogêneos e H uma matriz 3x3:

\[ \begin{bmatrix}x_0 & y_0 & 1_0\end{bmatrix}^T = \begin{bmatrix}h_{11} & h_{12} & h_{13} & h_{21} & h_{22} & h_{23} & h_{31} & h_{32} & h_{33}\end{bmatrix} \begin{bmatrix}x_1 & y_1 & 1_1\end{bmatrix}^T \tag{9.4} \]

Figura 9.3: Geometria de uma homografia - Temos nessa figura a representação de uma homografia que relaciona pontos entre dois planos de imagem de um mesmo plano no mundo. [67, p. 60].

E a partir da equação anterior podemos deduzir que:

\[ x_0 = \frac{h_{11}x_1 + h_{12}y_1 + h_{13}}{h_{31}x_1 + h_{32}y_1 + h_{33}} \text{ e } y_0 = \frac{h_{21}x_1 + h_{22}y_1 + h_{23}}{h_{31}x_1 + h_{32}y_1 + h_{33}} \tag{9.5} \] então:

\[ \begin{split} &h_{31}x_1x_0 + h_{32}y_1x_0 + h_{33}x_0 = h_{11}x_1 + h_{12}y_1 + h_{13}\\ &h_{31}x_1y_0 + h_{32}y_1y_0 + h_{33}x_0 = h_{21}x_1 + h_{22}y_1 + h_{23} \end{split} \tag{9.6} \]

que pode ser rearranjado em:

\[ \begin{split} &h_{31}x_1x_0 + h_{32}y_1x_0 + h_{33}x_0 - h_{11}x_1 - h_{12}y_1 + h_{13} = 0\\ &h_{31}x_1x_0 + h_{32}y_1x_0 + h_{33}x_0 - h_{21}x_1 + h_{22}y_1 + h_{23} = 0 \end{split} \tag{9.7} \]

e escrito em forma matricial:

\[ \begin{split} &\begin{bmatrix}-x_1 & -y_1 & -1 & 0 & 0 & 0 & x_1x_0 & y_1x_0 & x_0\end{bmatrix}h^T = 0 \\ &\begin{bmatrix}0 & 0 & 0 & -x_1 & -y_1 & -1 & x_1y_0 & y_1y_0 & y_0\end{bmatrix}h^T = 0 \end{split} \tag{9.8} \]

onde \(H = \begin{bmatrix}h_{11} & h_{12} & h_{13} & h_{21} & h_{22} & h_{23} & h_{31} & h_{32} & h_{33}\end{bmatrix}\)

Para que consigamos resolver esse sistema, e achar a homografia H, precisamos de no mínimo 4 pontos correspondentes em cada uma das imagens [68, p. 88], o que nos leva ao sistema de equações:

\[ \begin{bmatrix} -x_{11} & -y_{11} & -1 & 0 & 0 & 0 & x_{11}x_{01} & y_{11}x_{01} & x_{01}\\ 0 & 0 & 0 & -x_{11} & -y_{11} & -1 & x_{11}y_{01} & y_{11}y_{01} & y_{01}\\ -x_{12} & -y_{12} & -1 & 0 & 0 & 0 & x_{12}x_{02} & y_{12}x_{02} & x_{02}\\ 0 & 0 & 0 & -x_{12} & -y_{12} & -1 & x_{12}y_{02} & y_{12}y_{02} & y_{02}\\ -x_{13} & -y_{13} & -1 & 0 & 0 & 0 & x_{13}x_{03} & y_{13}x_{03} & x_{03}\\ 0 & 0 & 0 & -x_{13} & -y_{13} & -1 & x_{13}y_{03} & y_{13}y_{03} & y_{03}\\ -x_{14} & -y_{14} & -1 & 0 & 0 & 0 & x_{14}x_{04} & y_{14}x_{04} & x_{04}\\ 0 & 0 & 0 & -x_{14} & -y_{14} & -1 & x_{14}y_{04} & y_{14}y_{04} & y_{04} \end{bmatrix} = \begin{bmatrix} h_{11}\\ h_{12}\\ h_{13}\\ h_{21}\\ h_{22}\\ h_{23}\\ h_{31}\\ h_{32}\\ h_{33} \end{bmatrix} = 0 \tag{9.9} \]

Resolvendo o sistema de equações anterior, encontramos a matriz de homografia H entre as duas imagens. Algo importante a se notar é que o tamanho do sistema de equações, e por conseguinte o tamanho da matriz, não é fixo, pois cada ponto adicionará mais duas linhas (9.8) a matriz (9.9).

9.2.1 Transformação Linear Direta (DLT)

A transformação Linear Direta, comumente chamada pela sigla em inglês DLT(Direct Linear Transformation) é uma das maneiras de se calcular a estimação da matriz H. Esse método funciona da seguinte maneira [68, p. 91]:

1. Dado \(n >= 4\) pontos correspondentes entre dois planos 2d(imagens).
2. Para cada correspondência, crie uma matriz como a da equação (9.8) na forma matricial: \[ \begin{split} &\begin{bmatrix}-x_1 & -y_1 & -1 & 0 & 0 & 0 & x_1x_0 & y_1x_0 & x_0\end{bmatrix}\\ &\begin{bmatrix}0 & 0 & 0 & -x_1 & -y_1 & -1 & x_1y_0 & y_1y_0 & y_0\end{bmatrix} \end{split} \tag{9.10} \]
3. Junte todas as matrizes criadas em uma única matriz A de tamanho \(2n x 9\).
4. Obtenha a decomposição em valores singulares(Singular Value Decomposition - SVD) da matriz anterior, \(A=U\sum{V^T}\). O vetor singular unitário que corresponde ao menor valor singular é então a solução para h, ou seja, seja D diagonal com entradas positivas, ordenado em ordem decrescente na diagonal, então h será a última coluna de V.
5. Fazendo um reshape do vetor h, temos a matriz de homografia H.

9.3 Transformações de câmera

A formação de imagem a partir de uma câmera digital pode ser compreendida por uma sequência de transformações entre sistemas de coordenadas, que fazem a correspondência entres os pontos “P” do espaço tridimensional para os pontos “p” no plano da imagem. Para estudar estas transformações será utilizado como referência os quatros sistemas de coordenadas na Figura 9.4, apresentados por Carvalho et al. (2005) [69, p. 22]:

Figura 9.4: Sistemas de coordenadas. Relação entre os sistemas de coordenadas que determina a transformação da posição do objeto de interesse no SCM para a projeção na imagem (SCI). Outros sistemas intermediários são o Sistema de coordenadas da câmera (SCC) e o Sistema de coordenadas em pixel (SCP). [69, p. 22].

Sistema de coordenadas do mundo (SCM): é tridimensional com origem no ponto “O” e as posições são indicadas por (X, Y, Z).

Sistema de coordenadas da câmera (SCC): também é tridimensional, tem origem no centro óptico da câmera “Õ” e as coordenadas são referenciadas por (X’, Y’, Z’). O sistema é definido em relação ao plano de projeção \(\pi\), sendo que os eixos X’ e Y’ devem ser paralelos às bordas da imagem no plano, e o eixo Z’ é perpendicular de forma que entre o centro óptico (Õ) e a intersecção deste eixo com o plano exista uma distância f, que é a distância focal da câmera.

Sistema de coordenadas de imagem (SCI): um sistema bidimensional sobre o plano de projeção \(\pi\), com origem no ponto “C” e com coordenadas (x, y). A origem é definida pelo ponto que marca a projeção ortogonal do centro óptico da câmera (Õ) sobre o plano da imagem.

Sistema de coordenadas em pixel (SCP): também é um sistema bidimensional, com origem no canto superior (ou inferior) esquerdo da imagem e com posições representadas por (u, v). Identifica os pontos da imagem com relação a grade de pixels.

As etapas de transformações entre estes sistemas estão resumidas no esquema da Figura 9.5, em que ocorrem sucessivas mudanças de coordenadas dos pontos de interesse, inicialmente referenciados no sistema SCM como (X,Y, Z), passando por todos os sistemas até o nível de pixel (u, v). Entre as transformações realizadas, estão a translação, rotação, escala e projeções que podem ser descritas como combinações de operações matriciais na sua forma homogênea [70, p. 481], seguindo as abordagens descritas no tópico coordenadas homogêneas.

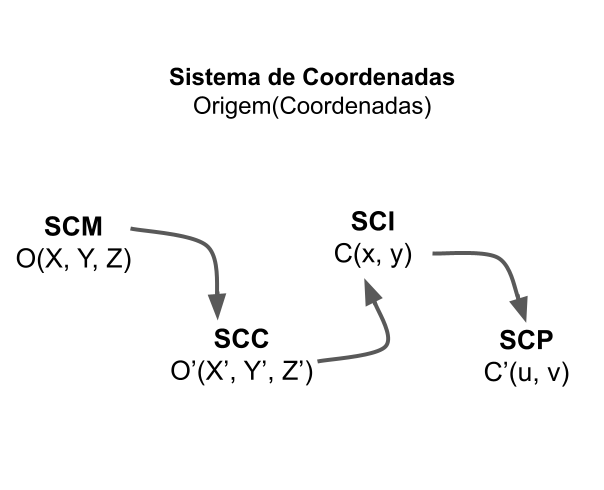
Figura 9.5: Mudanças de coordenadas. Etapas de transformação do referencial do objeto de interesse (SCM) para o sistema de coordenadas de pixel (SCP) no plano de projeção. São apresentados quatro sistemas de coordenadas - SCM, SCC, SCI, SCP - cada um com a identificação da origem e dos pontos, por exemplo, no SCM a origem é indicada por “O” e o ponto (X, Y, Z).

A passagem do referencial real (SCM) para o da câmera (SCC) pode ser descrita como:

\[ \tilde{P} = RP + T \tag{9.11} \]

em que ocorre a mudança de coordenada do ponto P (X, Y, Z) em SCM para a correspondência \(\tilde{P}\) (X’, Y’, Z’) em SCC. O vetor T é a posição da origem absoluta (O) no sistema SCC. A matriz R fornece a posição dos versores dos eixos do SCM com relação ao SCC [69, p. 23]. Em coordenadas homogêneas esta expressão é escrita:

\[ \begin{bmatrix} \tilde{X}\\ \tilde{Y}\\ \tilde{Z}\\ 1 \end{bmatrix} = \begin{bmatrix} R & T\\ 0 & 1 \end{bmatrix} \begin{bmatrix} X\\ Y\\ Z\\ 1 \end{bmatrix} \tag{9.12} \] Como os dois referenciais são ortogonais, R é uma matriz ortogonal (\(RR^t = I\)) e é possível determiná-la apenas com 3 parâmetros em vez de 9, que caracterizam a rotação que leva de um eixo a outro, geralmente tratados como componentes do vetor Rodriguez [69, p. 24]. Assim, para cada posição da câmera existem 6 parâmetros que descrevem o seu estado extrínseco, 3 referentes à matriz R e 3 do vetor T.

A mudança das coordenadas em relação a câmera (SCC) para o sistema da imagem (SCI) pode ser aproximada como uma projeção perspectiva em uma câmera pinhole com distância focal f [69, p. 24]:

\[ \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} = \begin{bmatrix} f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} \tilde{X}\\ \tilde{Y}\\ \tilde{Z}\\ 1 \end{bmatrix} \tag{9.13} \] Como esta transformação projetiva não é inversível, um ponto da imagem pode ser associado com uma infinidade de pontos no espaço, ou seja, o ponto (x, y) da imagem é tratado como a projeção de todos os pontos do espaço que atendem a forma \(\lambda(x, y, f)\), em que \(\lambda != 0\) [69, p. 24].

O último nível de transformação que consideramos é do plano de formação da imagem (SCI) para a matriz retangular dos pixels (SCP):

\[ \begin{bmatrix} u\\ v\\ 1 \end{bmatrix} = \begin{bmatrix} s_x & \tau & u_c\\ 0 & s_y & v_c\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \tilde{X}\\ \tilde{Y}\\ \tilde{Z}\\ 1 \end{bmatrix} \tag{9.14} \] Os elementos \(s_x\) e \(s_y\) são a quantidade de pixels por unidade de comprimento, nas direções horizontal e vertical, respectivamente. Na maior parte das câmeras, o espaçamento entre linhas e colunas da matriz são iguais, ou seja, os pixels são quadrados \(s_x = s_y\). Os valores \(u_c\) e \(v_c\) descrevem a posição, em pixels, da projeção ortogonal do centro óptico da câmera (O’) sobre o plano de projeção, indicado como a origem C do SCI. Geralmente, o ponto C está no centro da imagem e a origem do SCP está no canto, assim, \(u_c\) e \(v_c\) são iguais a metade das dimensões da imagem. O elemento \(\tau\) reflete o alinhamento das colunas de pixels com as linhas, mais especificamente, é a tangente do ângulo que as colunas formam com a perpendicular às linhas. Quando as colunas são perpendiculares às linhas, \(\tau = 0\).

Os cinco parâmetros (\(s_x, s_y, u_c, v_c, \tau\)) mais a distância focal (f) totalizam os seis parâmetros intrínsecos da câmera, que descrevem o seu funcionamento interno, enquanto que os seis parâmetros extrínsecos (elementos da matriz R e do vetor T) estabelecem a posição e a orientação. A dependência destas variáveis nas transformações indica que para determinadas aplicações na visão computacional, como no rastreamento e na reconstrução 3D, é necessário modelar estes valores [70, p. 479] . O processo da determinação dos parâmetros extrínsecos e intrínsecos da câmera é denominado calibração [65, p. 331].

As equações anteriores podem ser combinadas como multiplicações de matrizes para estabelecer uma transformação de coordenada de um ponto de interesse (SCM) à sua projeção no referencial da matriz de pixels da câmera (SCP):

\[ [p] = \begin{bmatrix} fs_x & f\tau & u_c\\ 0 & fs_y & v_c\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} R & T \end{bmatrix} \begin{bmatrix} P \end{bmatrix} \approx K \begin{bmatrix} R & T \end{bmatrix} \begin{bmatrix} P \end{bmatrix} \tag{9.15} \] em que “P” é a coordenada em SCM e “p” em SCP. A matriz K de calibração define os parâmetros intrínsecos da câmera, enquanto [R T] representa os extrínsecos [71]. Na prática os valores de f, \(s_x\) e \(s_y\) não são determinados individualmente por esta operação, pois estão combinados como produtos (\(fs_x\) e \(fs_y\)) [69, p. 26], assim, a matriz de calibração pode ser escrita como:

\[ K = \begin{bmatrix} f_x & c & u_c\\ 0 & f_y & v_c\\ 0 & 0 & 1 \end{bmatrix} \tag{9.16} \]

9.4 Distorção das lentes

Os parâmetros intrínsecos foram modelados com base em uma aproximação do comportamento das câmeras do tipo pinhole, entretanto, as lentes das câmeras reais podem apresentar distorções. Geralmente as distorções mais proeminentes nas imagens são do tipo geométrica, em que os pontos no plano da imagem são deslocados de onde deveriam ser projetados [65, p. 331]. A maior parte dos modelos empíricos de distorção consideram as distorções geométricas radiais e tangenciais [72].

Figura 9.6: Distorção radial. Este tipo de distorção faz com que as linhas retas pareçam curvadas, e o efeito é maior nas bordas. (a) Imagem com distorção radial. (b) Imagem sem distorção. [71, p. 3]

A distorção radial faz com que os pontos da imagem sejam transladados ao longo das linhas radiais a partir da origem do plano de projeção (C), fazendo com que as linhas retas pareçam curvadas como na Figura 9.6. A distorção radial se torna maior quanto mais longe os pontos estão do centro da imagem [72]. A imagem que deveria se formar no ponto (u, v) do plano de projeção é deslocada para o ponto (u’, v’) devido a distorção que pode ser avaliada como [69, p. 27]:

\[ (u', v') = (1 + d) (u, v) \tag{9.17} \] em que a distorção (d) depende da distância do ponto da imagem ao ponto de origem (C) descrita como:

\[ r = \sqrt{(x)^2 + (y )^2} \tag{9.18} \] A relação entre “r” e “d” pode ser modelada por uma função polinomial [69, p. 27]:

\[ d = k_1r^2 +k_2r^4 + k_3r^6 + … \tag{9.19} \] sendo \(k_n\) os coeficientes de distorção radial. A distorção tangencial acontece pelo desalinhamento da lente com o plano da imagem, que pode não estar perfeitamente paralela, fazendo com que algumas áreas da imagem pareçam mais próximas do que o esperado [72]. Considerando as distorções radiais e tangenciais o ponto na imagem é posicionado em:

\[ u' = u + \delta_u \text{, } v' = v + \delta_v \tag{9.20} \] em que os deslocamentos (\(\delta_u\), \(\delta_v\)) são modelados como [65, p. 330]:

\[ \begin{bmatrix} \delta_u\\ \delta_v \end{bmatrix} = \begin{bmatrix} u(k_1r^2 + k_2r^4 + k_3r^6 + ...)\\ v(k_1r^2 + k_2r^4 + k_3r^6 + ...) \end{bmatrix} + \begin{bmatrix} 2p_1uv + p_2(r^2 + 2u^2)\\ p_1(r^2 + 2v^2) + 2p_2uv \end{bmatrix} \tag{9.21} \] Geralmente, apenas 3 coeficientes (\(k_1, k_2, k_3\)) de distorção radial são suficientes para descrever a distorção radial, que juntamente com os 2 coeficientes tangenciais (\(p_1, p_2\)) são considerados como parâmetros intrínsecos adicionais, os parâmetros de distorção (\(k_1, k_2, k_3, p_1, p_2\)) [65, p. 330].

9.5 Calibração

Determinar os parâmetros intrínsecos e extrínsecos com base na equação (p = K [R T] [P]) envolve a resolução de um problema de otimização não linear. Geralmente, o problema é formulado como uma minimização de erro com base na diferença entre posições conhecidas da imagem (p) com os valores estimados (p’) utilizando como referência os parâmetros R, T, K e \(\delta\) da solução [69, p. 28]. Assim, os parâmetros intrínsecos são estabelecidos de forma que os pontos da imagem (p’) obtidos por uma câmera em calibração sejam os mais próximos dos pontos (p) conhecidos da imagem [69, p. 28]:

\[ \sum_{i=0}^n {||p'_i - p_i||^2} \tag{9.22} \] Na calibração devem ser utilizadas imagens de amostra de um padrão, como de um tabuleiro de xadrez (Figura 9.7), em que seja possível identificar automaticamente na imagem pontos cujas coordenadas sejam conhecidas [69, p. 29]. No caso do tabuleiro de xadrez, os pontos de referência são as interseções dos quadrados que possibilitam identificar tanto as coordenadas na imagem (p) quanto no real (P) [71, p. 12].

Para exemplificar as etapas de calibração utilizaremos como guia o material e o código disponibilizados na documentação do OpenCv [72]. As etapas de calibração que descreveremos seguem o método Zhang, que usa um padrão bidimensional, mas que é posicionado em diferentes posições do espaço [69, p. 39]. Na prática, as imagens são obtidas a partir de uma câmera estática e o tabuleiro é colocado em diferentes posições e orientações, sendo necessário pelo menos 10 imagens [72]. Em cada imagem são utilizados os mesmos pontos de referência, por exemplo, pela Figura 9.7 se identifica 9x6 pontos de interseção no tabuleiro, assim, a entrada do algoritmo segue a forma tamanho_tabuleiro = (9,6) .

Figura 9.7: Tabuleiro de Xadrez. Uma das imagens utilizadas como padrão para realizar a calibração da câmera. Os pontos de contato entre os quadrados de mesma cor são utilizados como posições de referência para o algoritmo de calibração. [72]

Uma abordagem que simplifica a aplicação dos algoritmos é considerar que o tabuleiro se mantém estacionário no plano XY e que é a câmera que se move, desta forma, não é preciso se preocupar com as coordenadas do terceiro eixo (Z= 0) [72]. Os valores de X e Y são definidos como a localização dos pontos no tabuleiro, e considerando o formato em grade, são identificados como (0,0), (1,0), (2,0),…, (8,5). No código, os pontos no referencial do espaço real são identificados como pontos objeto e no plano de projeção como pontos imagem.

As coordenadas dos pontos na imagem do tabuleiro podem ser determinadas pela função “cv.findChessboardCorners(imagem, tamanho_tabuleiro, flags)”, que recebe como entrada a imagem e o tamanho do tabuleiro. Esta função retorna as coordenadas dos pontos de referência na imagem (corners) e a variável “ret” recebe “True” quando isto acontece. Os pontos são salvos de acordo com as posições no tabuleiro, da esquerda para a direita e de cima para baixo.

ret, corners = cv.findChessboardCorners(imagem, (9,6), None)

Geralmente é utilizada a função “cv.cornerSubPix(imagem, corners, winSize, zeroZone, criterio)” para aumentar a acurácia do posicionamento dos pontos. A função “cornerSubPix” recebe a imagem e os pontos de referência calculados (corners) e avalia os pontos dentro uma vizinhança estabelecida pelo parâmetro “winSize”, que define a metade do comprimento da janela de pesquisa. O parâmetro “zeroZone” indica o tamanho da região em que os cálculos não são realizados, utilizado às vezes para evitar singularidades da matriz de autocorrelação. Quando “zeroZone = (-1,-1)”, esta estratégia não é utilizada, não existindo regiões “mortas”. Como o algoritmo da função “cornerSubPix” é iterativo é necessário estabelecer um critério de parada, como o número de interações e/ou acurácia. Após estabelecer os pontos da imagem é possível desenhá-los sobre o tabuleiro com a função “cv.drawChessboardCorners(imagem, tamanho_tabuleiro, corners, ret).

criterio = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001
corners = cv.cornerSubPix(imagem, corners, (11,11), (-1,-1), criterio)
cv.drawChessboardCorners(imagem, (9,6), corners, ret)

As coordenadas reais identificadas como pontos objeto e as coordenadas na imagem são repassadas como entradas da função “cv2.calibrateCamera(objectPoints, imagePoints, imageSize, flags)”. Esta função retorna os parâmetros intrínsecos e extrínsecos da câmera com base no método Zhang, o qual considera inicialmente nos cálculos uma aproximação da câmera pinhole e depois integra as distorções.

O problema da calibração se fundamenta em estabelecer os parâmetros das transformações que realizam o mapeamento da coordenada homogênea P=(X,Y, Z, 1) do real para a imagem p=(x, y, 1) [71, p. 11]:

\[ \lambda \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} = K \begin{bmatrix} r_1 & r_2 & r_3 & t \end{bmatrix} \begin{bmatrix} X\\ Y\\ Z = 0\\ 1 \end{bmatrix} K \begin{bmatrix} r_1 & r_2 & t \end{bmatrix} \begin{bmatrix} X\\ Y\\ 1 \end{bmatrix} \tag{9.23} \]

Ao adotar que o plano de calibração está sobre Z=0 podemos simplificar as coordenadas homogêneas dos pontos reais como (X, Y, 1), o que permite escrever a transformação de coordenadas como [71, p. 12]:

\[ \lambda \begin{bmatrix} x & y & 1 \end{bmatrix} = H \begin{bmatrix} X & Y & 1 \end{bmatrix} \tag{9.24} \] em que dado os pontos no plano padrão de calibração (P) e os pontos na imagem (p) é possível determinar uma Homografia (H), uma transformação projetiva entre planos, para cada imagem padrão. Assim, ao calcular a Homografia como indicado no tópico homografia se consegue estabelecer a seguinte relação:

\[ H = \lambda K\begin{bmatrix} r_1 & r_2 & T \end{bmatrix} \tag{9.3} \] O que permite determinar os parâmetros intrínsecos e extrínsecos da câmera. Os elementos da matriz de calibração (K) são estimados considerando a matriz simétrica \(B = K^{-T} K^{-1}\) de acordo com as expressões [71, p. 14]:

\[ \begin{split} &v_c = \frac{(B_{12}B_{13} - B_{11}B_{23})}{(B_{11}B_{22} - B_{12}^2)}\\ &\lambda = B_{33} - \frac{[B_{13}^2 + v_c(B_{12}B_{13} - B_{11}B_{23})]}{B_{11}}\\ &f_x = \sqrt{\frac{\lambda}{B_{11}}}\\ &f_y = \sqrt{\frac{\lambda B_{11}}{(B_{11}B_{22} - B_{12}^2)}}\\ &c = \frac{-B_{12}f_x^2f_y}{\lambda}\\ &u_c = \frac{\lambda v_c}{f_x} - \frac{B_{13}f_x^2}{\lambda} \end{split} \tag{9.25} \] Após determinar os cinco elementos da matriz de calibração (\(v_c, u_c, f_x, f_y, c\)) e o fator de escala (\(\lambda\)) calculam-se os parâmetros extrínsecos (R, T) [71, p. 15]:

\[ \begin{split} &r_1 = \frac{1}{\lambda}K^{-1}h_1\\ &r_2 = \frac{1}{\lambda}K^{-1}h_2\\ &r_3 = r_1 x r_2\\ &t = \frac{1}{\lambda}K^{-1}h_3\\ \end{split} \tag{9.26} \] As distorções podem ser calculadas com base nos valores estimados das posições (p’) utilizando os parâmetros da calibração, que apresentam distorções, com os pontos ideais da imagem (p). Os modelos de distorções radiais e tangenciais apresentados em são reescritos na forma matricial, o que permite determinar uma solução por mínimos quadrados com os resultados para os coeficientes de distorção radial (\(k_1, k_2, k_3\)) e tangencial (\(p_1, p_2\)) [69, p. 44].

Considera-se que os parâmetros intrínsecos são os mesmos em todas as imagens padrão, e que somente os parâmetros extrínsecos se alteram quando a imagem é reposicionada [72]. Todas as etapas anteriores são resolvidas por uma única função no OpenCV:

ret, cameraMatrix, dist, rvecs, tvecs = cv.calibrateCamera(objpoints, imgpoints, imagem.shape[::-1], None, None)

em que se tem como saída da função a matriz de calibração (cameraMatriz) e os coeficientes de distorções (dist), que valem para todas as imagens, e o vetor de rotação R (rvecs) e de translação T (tvecs) que são calculados por padrão.

Refêrencias

[19] M. Nixon e A. Aguado, Feature extraction and image processing for computer vision. Academic press, 2019.

[65] P. Corke, Robotics, Vision and Control Fundamental Algorithms in MATLAB, 2º ed. Gewerbestrasse, Suiça: Springer, 2017.

[66] W. Commons, “Railroad tracks "vanishing" into the distance”. 2006, [Online]. Disponível em: https://commons.wikimedia.org/wiki/File:Railroad-Tracks-Perspective.jpg.

[67] R. Szeliski, Computer vision: algorithms and applications. Springer Science & Business Media, 2010.

[68] R. Hartley e A. Zisserman, “Multiple view geometry in computer”, Vision, 2nd ed., New York: Cambridge, 2003.

[69] P. C. Carvalho et al., “Fotografia 3D – 25 Coloquio Brasileiro de Matematica”, Rio de Janeiro: Associação Instituto de Matematica Pura e Aplicada, IMPA, 2005.

[70] E. R. Davies, Computer and Machine Vision: Theory, Algorithms, Practicalities, 4º ed. Waltham, Estados Unidos: Elsevier, 2012.

[71] M. C. dos Santos, “Revisão de Conceitos em Projeção, Homografia, Calibração de Câmera, Geometria Epipolar, Mapas de Profundidade e Varredura de Planos”. Disciplina Visão Computacional, Unicamp, sob orientação do Prof. Dr. Helio Pedrini., São Paulo, 2012, [Online]. Disponível em: https://www.ic.unicamp.br/~rocha/teaching/2012s1/mc949/aulas/additional-material-revision-of-concepts-homography-and-related-topics.pdf.

[72] “Camera Calibration”. Website do OpenCV, [Online]. Disponível em: https://docs.opencv.org/master/dc/dbb/tutorial_py_calibration.html.